On this post we explain how to do the matrix addition and subtraction. In addition, you will see examples of addition and subtraction of matrices. Also, you will find problems to practice these matrix operations. And, finally, we will show you all the properties of the matrix addition.
Table of Contents
How to add and subtract matrices?
To add (or subtract) two matrices, add (or subtract) the elements that are in the same position. Thus, two matrices can only be added or subtracted if they both have the same dimension.
Examples of adding and subtracting matrices
Let A and B be two square 2×2 matrices, the addition and the subtraction of them are calculated as follows:

So the rules of adding and subtracting matrices are simple: we simply have to add or subtract the corresponding entries and place the result of the operation in the same position.
Moreover, to add or subtract two matrices both of them must have the same dimension. For example, the following matrices cannot be added because they are of different sizes: the first one is a 2×2 dimension matrix and the second one is a 3×2 dimension matrix.
As a curiosity, there is another type of matrix addition called Kronecker sum, although it very rare and it is not used much in linear algebra.
Practice addition and subtraction of matrices
Problem 1
Add the following 2×2 dimension matrices:
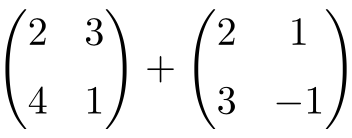
To add the two square matrices of order 2 we have to add the corresponding entries:
Problem 2
Subtract the following 3×2 matrices:
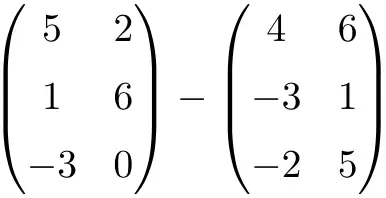
Even though the matrices are not square, we can subtract them because they have the same dimension:
Problem 3
Find the following 3×3 matrix addition:
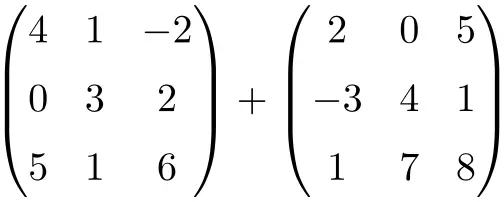
To calculate the matrix sum we have to add the elements that are in the same position:
Problem 4
Calculate the following additions and subtractions of 2×2 matrices:
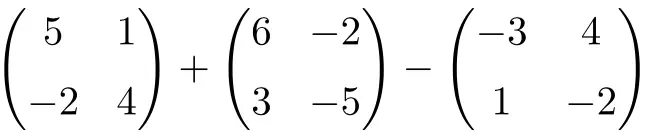
In this case we have an addition and a subtraction of matrices. So we add the matrices on the left first:
And then we subtract the matrices:
Problem 5
Add and subtract the following 3×3 dimension matrices:
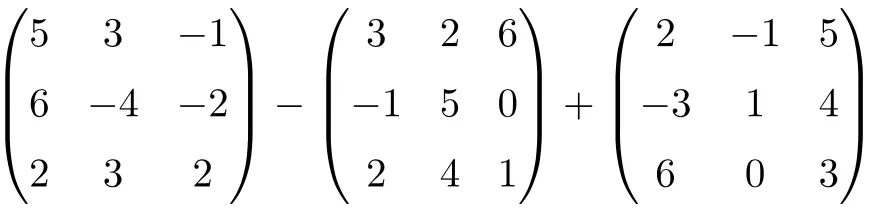
First, we solve the matrix subtraction:
And finally we do the sum of matrices:
Now that you know how to add and subtract matrices, you should see 2×2 matrix multiplication.
Properties of matrix addition
Matrix addition satisfies the following characteristics:
- The matrix addition has the commutative property:
Therefore, the order in which we add the matrices is indifferent. To prove this property we are going to add two matrices changing their order, you will see that the result is the same.
So we proceed to add two matrices:
Note that if we reverse the order in which the matrices have been added, the result of the sum remains the same:
- Another property of the matrix addition is the opposite element:
That is, if we add a matrix plus the same matrix but with all its elements changed sign, the result will be the null matrix. For example:
- The matrix addition also has the property of the neutral element:
This property is the most obvious one, and it means that any matrix plus a matrix full of zeros results in the same matrix:
- The matrix addition has the associative property:
Therefore, the order in which we add matrices is indifferent. Take a look at the following example, where we add 3 matrices with a different order and the result is the same:
