▷ How to multiply polynomials by monomials and polynomials

On this post we explain how to multiply polynomials. You will see examples of multiplications of polynomials and, also, exercises solved step by step. Finally, you will find what are the properties of the multiplication of polynomials.

However, to understand the concept of multiplication of polynomials, we will go from the most simple product to the most complicated, that is, we will start with how to multiply a polynomial by a constant, then we will see how to multiply a polynomial by a monomial, and finally, we will explain how to multiply two or more polynomials.

Table of Contents

Multiplying polynomials by constants

The product of a scalar (or real number) by a polynomial is quite easy to solve, you simply have to multiply the constant by the coefficient of each term of the polynomial .

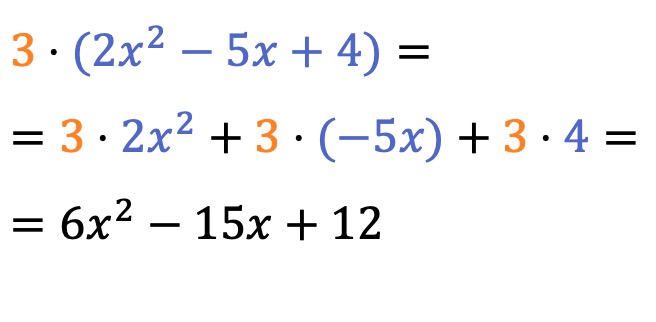
The multiplication sign in front of the parentheses can be omitted.

$\begin{array}{l} -2\cdot (5x^4-6x^2) = \\[2ex] =-2 (5x^4-6x^2)= \\[2ex] = -10x^4+12x^2 \end{array}$

Multiplying polynomials by monomials

Before seeing how to multiply a polynomial by a monomial, let’s first remember how to multiply monomials, because it is necessary to know it to be able to do this type of polynomial operation.

The product of two monomials consists of multiplying their coefficients and adding the exponents of the variables that are equal. Take a look at the following example:

$3x^2\cdot4x^5=(3\cdot4)x^{2+5}=12x^7$

Now let’s see how to multiply a polynomial by a monomial:

To multiply a monomial by a polynomial, multiply the monomial by each term of the polynomial.

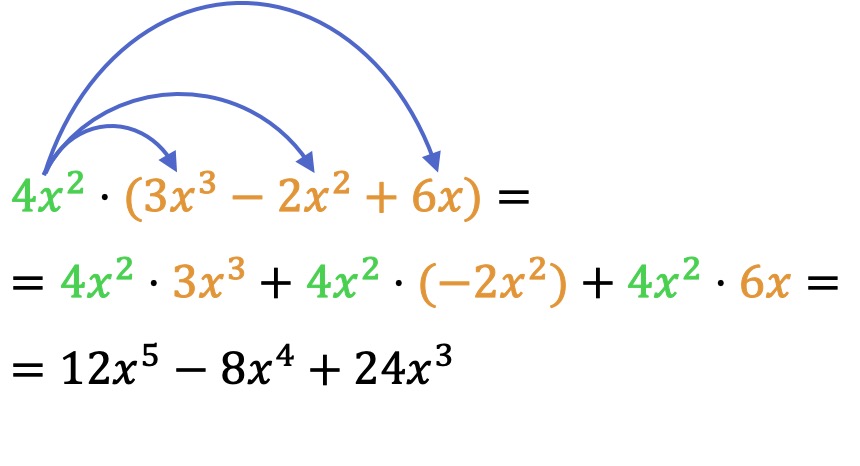
The multiplication sign can also be omitted:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Note in the previous example that when we multiply monomials or polynomials we must also take into account the sign rules. In fact, a typical mistake in the product of monomials and polynomials is to miss the sign of a term.

Multiplying polynomials by polynomials

Once we know how to multiply polynomials by constants and by monomials, let’s see how to multiply two or more polynomials.

To solve a multiplication of polynomials:

Multiply each term of the first polynomial by all the terms of the second polynomial.
Add (or subtract) the monomials that have the same degree (like terms).

We are going to calculate the following multiplication of polynomials step by step as an example:

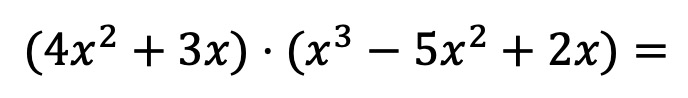
First, we have to multiply each element of the first polynomial by each term of the second polynomial:

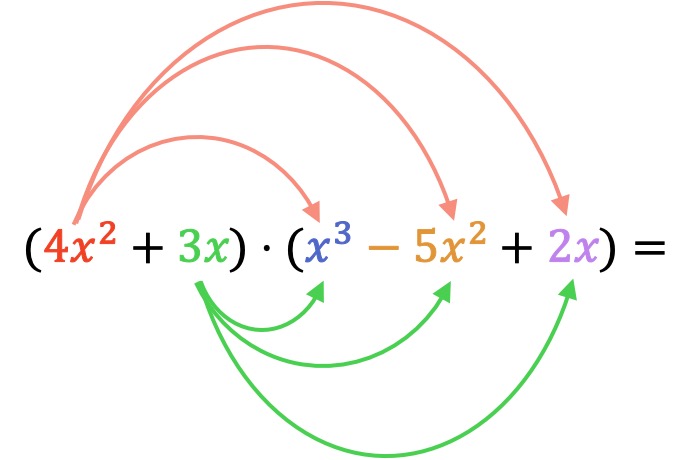
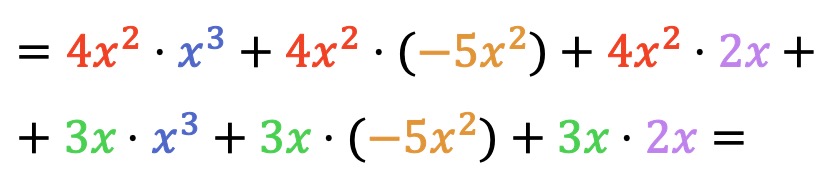
Now we compute all the multiplications of monomials:

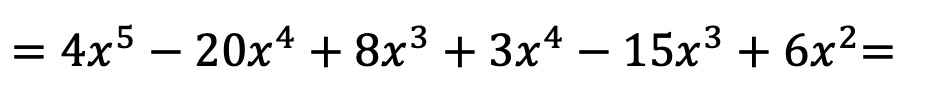
Once we have multiplied the polynomials, we simply have to combine the like terms, in other words, the terms with the same letter and the same exponent:

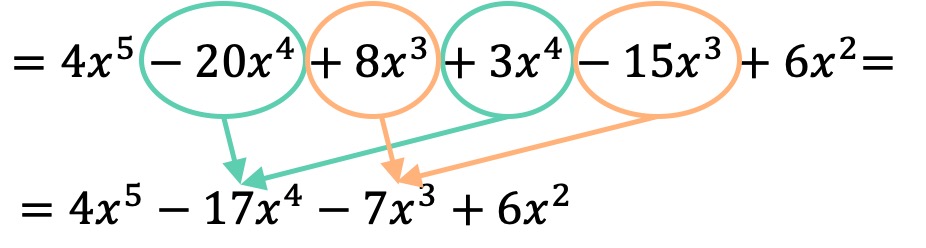
So the result of the polynomial multiplication is:

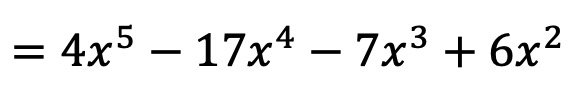
Vertical multiplication of polynomials

We have just seen how to multiply a polynomial by another polynomial horizontally, but it can also be done in a more classical way: multiplying polynomials vertically, also called long multiplication of polynomials. So let’s see how to apply this method by solving an example.

If we want to multiply the following two polynomials vertically:

$(5x^2+3x-4) \cdot (2x^2-x)$

The first thing we must do is place one polynomial below the other, in the form of algebraic multiplication of polynomials:

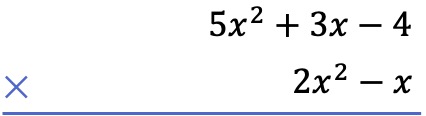
Secondly, we multiply each term of the bottom polynomial by each term of the top polynomial, and we arrange the results ordered by columns from highest to lowest degree:

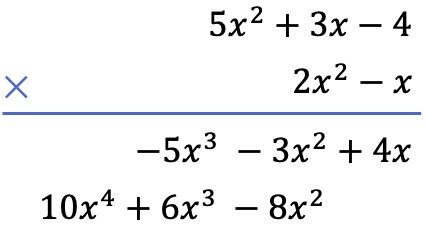
And finally, we add the terms that are vertically aligned:

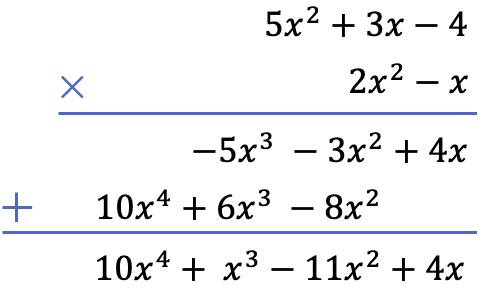
Properties of multiplication of polynomials

The multiplication of polynomials has the following characteristics:

Commutative property: the order of the multiplication of polynomials does not change the result of the product.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

Associative Property: when three or more polynomials are multiplied, the result of the product is the same regardless of how the factors are grouped:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Distributive property: the sum of two polynomials multiplied by a third polynomial is equal to the sum of each addend by the third polynomial.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

The degree of the polynomial resulting from a multiplication of two polynomials is equal to the sum of the degrees of the two polynomials that were being multiplied.

Practice problems on multiplying polynomials

So that you can practice, below you have several solved exercises of multiplications of polynomials. You can try to solve them yourself and check your results with the proposed solution. Then you can ask us any questions you have in the comments section, we will be glad to help you.

Problem 1

Calculate the following products of polynomials and constants:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

See solution

To find the multiplication of a polynomial by a constant we must multiply the number by the coefficient of each term of the polynomial. Thus:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Problem 2

Solve the following multiplications between polynomials and monomials:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

See solution

To solve the multiplication of a polynomial by a monomial we must multiply the monomial by each term of the polynomial. Therefore:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Problem 3

Determine the result of the following multiplications of polynomials:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

See solution

To compute a multiplication of two polynomials we must multiply each element of the first polynomial by each element of the second polynomial, and then combine the like terms. Thus:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Problem 4

Find the result of the following products of polynomials:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

See solution

To calculate a multiplication of two polynomials we must multiply each element of the first polynomial by each element of the second polynomial, and then add the like terms. Therefore:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Problem 5

Multiply the following polynomials:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

See solution

To do the product of two polynomials, you have to multiply each term of the first polynomial by each term of the second polynomial, and then combine the like terms. Therefore:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Problem 6

Solve the following multiplication of 3 polynomials:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

See solution

The operation of the problem consists of 2 multiplications of polynomials, in particular, it is composed of two binomials and a trinomial. So we first have to solve a product and then multiply the result by the remaining polynomial.

So we calculate the multiplication of the first binomial and the trinomial:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

And now we solve the other multiplication:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Problem 7

Multiply the following polynomials with rational coefficients (with fractions):

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

See solution

Although the polynomials have fractions, it is still a multiplication of two polynomials. So it must be solved like any polynomial product: multiplying all the elements and then combining like terms.

So, we multiply the polynomials:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

And finally, we add (or subtract) the like terms:

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

In order to do this exercise well, it was important that you knew how to do operations with fractions. But if you have any questions, you can ask them below in the comments.

Multiplying polynomials by constants

Multiplying polynomials by monomials

Multiplying polynomials by polynomials

Vertical multiplication of polynomials

Properties of multiplication of polynomials

Practice problems on multiplying polynomials

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Leave a Comment Cancel Reply