How to find the inverse of a matrix (formula and examples)

We explain what the inverse of a matrix is and how to find it. You will learn the formulas to calculate the inverse of a 2×2 matrix and the inverse of a 3×3 matrix. Also, you will see several solved examples. And finally, we explain the properties of the inverse matrix.

Table of Contents

What is the inverse of a matrix?

The definition of the inverse of a matrix is as follows:

The inverse of a matrix is a matrix that multiplied by the original matrix results in the identity matrix, regardless of the order of the matrix multiplication.

Thus, let A be a square matrix, the inverse of matrix A is denoted by A^-1 and satisfies:

A·A^-1=I

A^-1·A=I

Where I is the identity matrix.

When can a matrix be inverted?

The easiest way to determine the invertibility of a matrix is by computing its determinant:

If the determinant of the matrix is nonzero, the matrix is invertible.
If the determinant of the matrix is equal to 0, the matrix cannot be inverted. In such a case, the matrix is singular or degenerate.

How to find the inverse of a 2×2 matrix

The formula to find the inverse of a 2×2 matrix is as follows:

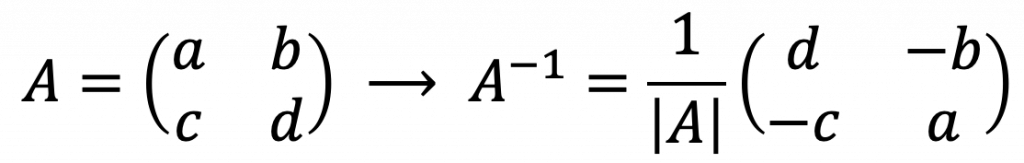
As you can see, inverting a 2×2 dimension matrix is simple: you only have to solve the determinant of the matrix (|A|), switch the elements on the main diagonal, and change the sign of the elements on the secondary diagonal.

Example

We are going to calculate the inverse of the following 2×2 square matrix:

$\displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}$

First, we take the determinant of the 2×2 matrix:

$\displaystyle\begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}$

Now we apply the formula of the inverse matrix:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}$

And we multiply the matrix by the fraction:

$\displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}$

So the inverse of matrix A is:

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}$

As you can see, inverting a matrix with this formula is very fast, but it can only be used for 2×2 matrices.

Practice

Problem 1

Invert the following 2×2 dimension matrix:

$\displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}$

See solution

First of all, we compute the determinant of the matrix:

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}$

Secondly, we use the formula to find the inverse matrix:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}$

Therefore, the inverse of matrix A is:

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}$

Problem 2

Find the inverse of the following matrix of order 2:

$\displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}$

See solution

First we compute the determinant of the matrix:

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}$

Then we use the formula of the inverse matrix:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}$

And finally, we perform the multiplication:

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}$

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}$

Problem 3

Perform the matrix inversion of the following 2×2 dimension matrix:

$\displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}$

See solution

The determinant of matrix A is:

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}$

Now we apply the formula to calculate the inverse of matrix A:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}$

And we solve the product of the fraction and the matrix:

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}$

How to find the inverse of a 3×3 matrix

The formula to calculate the inverse of a 3×3 matrix is as follows:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

Where:

$\displaystyle \begin{vmatrix} A \end{vmatrix}$ is the determinant of matrix A.
$\text{Adj} (A)$ is the adjugate or adjoint of matrix A.

Next we will see how to calculate the inverse of a 3×3 matrix by solving an exercise step by step:

Example

Find the inverse of the following 3×3 matrix:

$\displaystyle A=\begin{pmatrix}1&3&1\\[1.1ex] 0&3&1\\[1.1ex]4&2&0\end{pmatrix}$

To determine the inverse of the matrix, we have to apply the following formula:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

Therefore, we have to calculate the determinant of the matrix and verify that it is different from 0. So we evaluate the determinant of the 3×3 matrix using cofactor expansion:

$\begin{aligned}|A|=\begin{vmatrix}1&3&1\\[1.1ex] 0&3&1\\[1.1ex]4&2&0\end{vmatrix}& =1\cdot \begin{vmatrix}3&1\\[1.1ex]2&0\end{vmatrix}-3\cdot \begin{vmatrix} 0&1\\[1.1ex]4&0\end{vmatrix}+1 \cdot \begin{vmatrix}0&3\\[1.1ex]4&2\end{vmatrix}\\ &=1\cdot \Bigl[0-2\Bigr]-3\cdot\Bigl[0-4\Bigr]+1\cdot\Bigl[0-12\Bigr]\\[2ex]&=-2+12-12\\[2ex]&=-2 \end{aligned}$

The determinant of the matrix is not 0, so the matrix is invertible.

Therefore, substituting the value of the determinant in the formula, the inverse of the matrix will be:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

$\displaystyle A^{-1} = \cfrac{1}{-2} \cdot \text{Adj}(A)$

Now we have to calculate the adjoint of matrix A. To do this, we have to replace each element of matrix A by its cofactor in order to obtain the cofactor matrix, and then transpose the cofactor matrix.

Remember that the formula to compute the i, j cofactor of a matrix is as follows:

$C_{i,j}=(-1)^{i+j}\cdot M_{ij}$

Where M_ij is the i, j minor of the matrix, that is, the determinant that results from deleting the i-th row and the j-th column of the matrix.

So the cofactors of the elements of matrix A are:

$\displaystyle A=\begin{pmatrix}1&3&1\\[1.1ex] 0&3&1\\[1.1ex]4&2&0\end{pmatrix}$

$\text{Cofactor of 1} \ \longrightarrow \ \displaystyle C_{11}=(-1)^{1+1}\cdot\begin{vmatrix}3&1\\[1.1ex]2&0\end{vmatrix} =1\cdot (-2) =-2$

$\text{Cofactor of 3} \ \longrightarrow \ \displaystyle C_{12}= (-1)^{1+2}\cdot\begin{vmatrix}0&1\\[1.1ex]4&0\end{vmatrix} = -1 \cdot (-4) = 4$

$\text{Cofactor of 1} \ \longrightarrow \ \displaystyle C_{13}= (-1)^{1+3}\cdot\begin{vmatrix}0&3\\[1.1ex]4&2\end{vmatrix} = 1 \cdot (-12) =-12$

$\text{Cofactor of 0} \ \longrightarrow \ \displaystyle C_{21}= (-1)^{2+1}\cdot\begin{vmatrix}3&1\\[1.1ex]2&0\end{vmatrix} = -1 \cdot (-2)=2$

$\text{Cofactor of 3} \ \longrightarrow \ \displaystyle C_{22}= (-1)^{2+2}\cdot\begin{vmatrix}1&1\\[1.1ex]4&0\end{vmatrix} = 1 \cdot (-4)=-4$

$\text{Cofactor of 1} \ \longrightarrow \ \displaystyle C_{23}=(-1)^{2+3}\cdot\begin{vmatrix}1&3\\[1.1ex]4&2\end{vmatrix} = -1 \cdot (-10)=10$

$\text{Cofactor of 4} \ \longrightarrow \ \displaystyle C_{31}= (-1)^{3+1}\cdot\begin{vmatrix}3&1\\[1.1ex]3&1\end{vmatrix} = 1 \cdot 0=0$

$\text{Cofactor of 2} \ \longrightarrow \ \displaystyle C_{32}= (-1)^{3+2}\cdot\begin{vmatrix}1&1\\[1.1ex]0&1\end{vmatrix} = -1 \cdot 1 =-1$

$\text{Cofactor of 0} \ \longrightarrow \ \displaystyle C_{33}=(-1)^{3+3}\cdot\begin{vmatrix}1&3\\[1.1ex] 0&3\end{vmatrix} = 1 \cdot 3 =3$

Once we have calculated all the cofactors, we simply have to replace each entry of A by its cofactor:

$\displaystyle\displaystyle C=\begin{pmatrix}-2&4&-12\\[1.1ex]2&-4&10\\[1.1ex]0&-1&3\end{pmatrix}$

And we transpose the cofactor matrix to find the adjugate matrix:

$\displaystyle\displaystyle\text{Adj}(A)=C^T=\begin{pmatrix}-2&2&0\\[1.1ex]4&-4&-1\\[1.1ex]-12&10&3\end{pmatrix}$

Thus, we substitute the adjugate matrix in the formula of the inverse matrix:

$\displaystyle A^{-1}=\cfrac{1}{-2} \cdot \text{Adj}(A)$

$\displaystyle A^{-1}=\cfrac{1}{-2} \cdot \begin{pmatrix}-2&2&0\\[1.1ex]4&-4&-1\\[1.1ex]-12&10&3\end{pmatrix}$

And finally, we multiply each term in the matrix by the fraction:

$\displaystyle A^{-1}=\begin{pmatrix}\frac{-2}{-2}&\frac{2}{-2}&\frac{0}{-2}\\[2ex]\frac{4}{-2}&\frac{-4}{-2}&\frac{-1}{-2}\\[2ex]\frac{-12}{-2}&\frac{10}{-2}&\frac{3}{-2}\end{pmatrix}$

$\displaystyle A^{-1}=\begin{pmatrix}1&-1&0\\[2ex]-2&2&\frac{1}{2}\\[2ex]6}&-5&-\frac{3}{2}\end{pmatrix}$

Once we have seen how to compute the inverse of a 3×3 matrix, you can practice with the following exercises solved step by step to fully understand the concept.

Practice

Problem 4

Invert the following 3×3 dimension matrix by the adjoint matrix method:

$\displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}$

See solution

The inverse matrix formula is:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

First we solve the determinant of the matrix using cofactor expansion:

$\begin{aligned}|A|=\begin{vmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{vmatrix}& =2\cdot \begin{vmatrix}4&1\\[1.1ex] 1&-3\end{vmatrix}-3\cdot \begin{vmatrix}1&1\\[1.1ex]2&-3\end{vmatrix}+(-2)\cdot \begin{vmatrix}1&4\\[1.1ex] 2&1\end{vmatrix}\\ &=2\cdot \Bigl[-12-1\Bigr]-3\cdot\Bigl[-3-2\Bigr]-2\cdot\Bigl[1-8\Bigr]\\[2ex]&= 2\cdot (-13)-3\cdot(-5)-2\cdot(-7)\\[2ex]&=-26+15+14\\[2ex]&=3 \end{aligned}$

The determinant is nonzero, therefore, the matrix can be inverted.

Once we have solved the determinant, we find the cofactor of each element of matrix A:

$\text{Cofactor of 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}$

$\text{Cofactor of 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}$

$\text{Cofactor of -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}$

$\text{Cofactor of 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}$

$\text{Cofactor of 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}$

$\text{Cofactor of 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}$

$\text{Cofactor of 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}$

$\text{Cofactor of 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}$

$\text{Cofactor of -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}$

Now we calculate the cofactor matrix by replacing each element by its cofactor:

$\displaystyle C= \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}$

And we transpose the cofactor matrix to obtain the adjoint of matrix A:

$\displaystyle\text{Adj}(A)=C^T=\begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}$

So the inverted matrix is:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}$

$\displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}$

Problem 5

Find the inverse of the following matrix of order 3 by the adjoint matrix algorithm:

$\displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}$

See solution

The formula to find the inverse of a matrix of order 3 is as follows:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

So, first we have to calculate the determinant of the matrix to check the invertibility of the matrix:

$\begin{aligned}|A|=\begin{vmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{vmatrix}& =4\cdot \begin{vmatrix}3&2\\[1.1ex] 8&1\end{vmatrix}-5\cdot \begin{vmatrix}-1&2\\[1.1ex] 3&1\end{vmatrix}+(-1)\cdot \begin{vmatrix}-1&3\\[1.1ex] 3&8\end{vmatrix}\\ &=4\cdot \Bigl[3-16\Bigr]-5\cdot\Bigl[-1-6\Bigr]-1\cdot\Bigl[-8-9\Bigr]\\[2ex]&= 4\cdot (-13)-5\cdot(-7)-1\cdot(-17)\\[2ex]&=-52+35+17\\[2ex]&=\bm{0} \end{aligned}$

The determinant of matrix A is equal to zero so the matrix is non-invertible, in other words, the inverse of matrix A does not exist.

Problem 6

Perform the matrix inversion of the following 3×3 dimension matrix by the adjugate matrix method:

$\displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}$

See solution

To invert the 3×3 matrix we have to apply the following formula:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

First we evaluate the determinant of the 3×3 matrix:

$\begin{aligned}|A|=\begin{vmatrix}1&4&-3\\[1.1ex]-2&1&0\\[1.1ex]-1&-2&2\end{vmatrix}& =1\cdot \begin{vmatrix}1&0\\[1.1ex]-2&2\end{vmatrix}-4\cdot \begin{vmatrix}-2&0\\[1.1ex]-1&2\end{vmatrix}+(-3)\cdot \begin{vmatrix}-2&1\\[1.1ex]-1&-2\end{vmatrix}\\ &=1\cdot \Bigl[2-0\Bigr]-4\cdot\Bigl[-4-0\Bigr]-3\cdot\Bigl[4-(-1)\Bigr]\\[2ex]&= 1\cdot 2-4\cdot(-4)-3\cdot5\\[2ex]&=2+16-15\\[2ex]&=3 \end{aligned}$

The determinant is nonzero, therefore, the matrix can be inverted.

Once we have solved the determinant, we find the cofactors of all the elements of matrix A:

$\displaystyle \text{Cofactor of 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}$

$\displaystyle \text{Cofactor of 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}$

$\displaystyle \text{Cofactor of -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}$

$\displaystyle \text{Cofactor of -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}$

$\displaystyle \text{Cofactor of 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}$

$\displaystyle \text{Cofactor of 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}$

$\displaystyle \text{Cofactor of -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}$

$\displaystyle \text{Cofactor of -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}$

$\displaystyle \text{Cofactor of 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}$

Now we calculate the cofactor matrix by replacing each element of matrix A by its cofactor:

$\displaystyle C=\begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}$

We transpose the cofactor matrix to find the adjugate matrix:

$\displaystyle\text{Adj}(A)=C^T=\begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}$

And we apply the formula of the inverse of a 3×3 matrix:

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \text{Adj}(A)$

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}$

$\displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}$

$\displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} &1 \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} &2 \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} &3\end{pmatrix}$

Properties of the inverse matrix

The inverse matrix has the following characteristics:

The inverse of a matrix is unique. That is, if the matrix is invertible, it only exists one inverse matrix.

The inverse of the inverse matrix results in the original matrix:

$\left(A^{-1}\right)^{-1} = A$

The inverse of a matrix multiplication is equal to the product of the inverses of the matrices but changing their order of multiplication.

$\left(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}$

Transposing a matrix first and then finding the inverse of the matrix is the same as first calculating the inverse of the matrix and then transposing it.

$\left(A^T\right)^{-1} = \left(A^{-1}\right)^T$

The determinant of the inverse of a matrix equals to the reciprocal of the determinant of the original matrix.

$\displaystyle det\left(A^{-1}\right) =\bigl( det(A) \bigr) ^{-1} = \cfrac{1}{det(A)}$

If a matrix is invertible, the following equation holds for a scalar multiplication:

$(k\cdot A)^{-1}=k^{-1}\cdot A^{-1}$

Solving a system of equations with the inverse matrix

Now you may be wondering… what is the inverse matrix for? Is it really used for something?

Well, one of the applications of the inverse matrix is the resolution of systems of linear equations. Let’s see an example of how to do it:

$\left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}$

A system of equations can be expressed with matrices:

$\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}$

We can verify that these matrices correspond to the system of equations by multiplying the matrices, since we would obtain the two equations of the system.

Now, to simplify the following steps, we will name A the square matrix that has the coefficients of the unknowns, X the column matrix with the unknowns, and B the column matrix with the independent terms:

$\displaystyle AX=B$

So matrix X is the unknown of the matrix equation.

This procedure is based on the definition of the inverse matrix: any matrix multiplied by its inverse is equal to the identity (or unit) matrix. Therefore, we can easily solve for the unknown matrix X by multiplying both sides of the equation by the inverse of matrix A:

$\displaystyle AX=B$

$\displaystyle A^{-1}\cdot AX=A^{-1}\cdot B$