On this post you will find how to do the division of polynomials. You will also see examples of divisions of polynomials and problems with answers to practice. Finally, you will find the properties of this polynomial operation.
Table of Contents
Division of polynomials
Before seeing how to divide two polynomials, we are going to briefly review the concepts of polynomial division, so that later it is easier to understand the method.
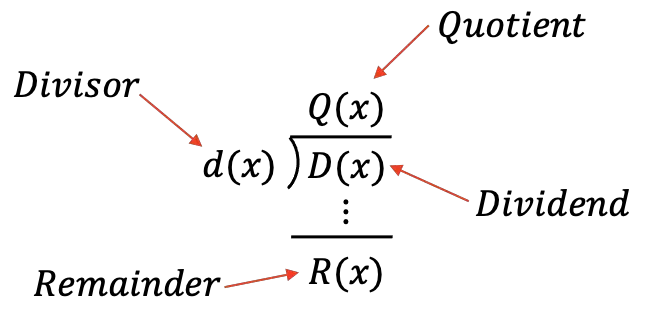
There are 4 polynomials involved in a division of polynomials:
- Dividend: the polynomial that is divided.
- Divisor: the polynomial that divides the dividend.
- Quotient: the result of dividing the dividend by the divisor.
- Remainder: the polynomial “left over” after dividing the two polynomials.
Furthermore, the following equation holds for every division of polynomials:
And we say that a division of polynomials is exact (or even) when the remainder is null. In such a case, the dividend polynomial is equal to the divisor multiplied by the quotient.
Now that we have seen what the polynomial division is, let’s see how to divide a polynomial by a polynomial.
Division of polynomials by polynomials
To divide two polynomials, we must apply a procedure called long division of polynomials. So let’s see how to divide polynomials by polynomials using long division method by solving an example step by step:
- Calculate the result of dividing the following two polynomials:
The first thing we must do is place the polynomials in division form. To do so, we write the denominator of the fraction, then a and finally the denominator with a line above:
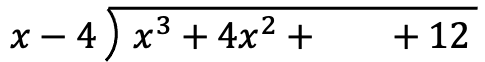
Note that if a polynomial does not have a monomial of a certain degree, we have to leave a blank place. For example, the polynomial does not have a term of degree 1, so there is a blank space in its place.
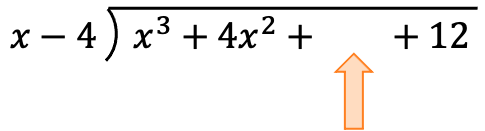
Once we have arranged the polynomials, we are going to calculate the quotient. And to find the first term of the quotient we have to divide the first term of the dividend by the first term of the divisor:
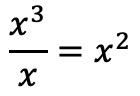
And we put the result of the division in the place of the quotient:
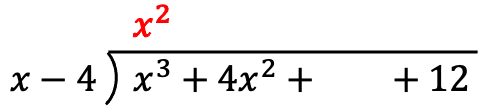
Now we multiply the term of the quotient by each element of the divisor, and we put the result of each multiplication below the dividend in its corresponding column:
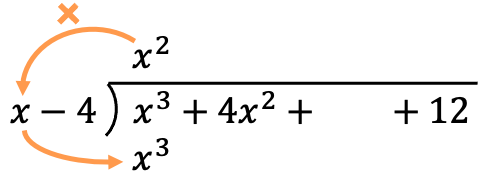

As in all operations with polynomials, it is important to order the polynomials from highest to lowest degree so that all terms of the same degree are located in the same column.
Once we have placed the results of the multiplications, we subtract the terms that are vertically aligned.
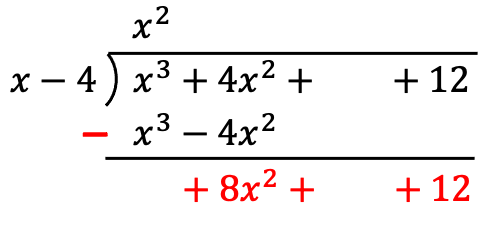
Remember that in the subtraction of polynomials we have to change the sign of the terms below! For example,
Note that when doing this subtraction, the coefficient with the highest degree cancels out and, therefore, we have one less term in the dividend.
Now we have to repeat the same procedure until we can’t bring down any other term from the dividend.
So we divide the first term of the dividend by the first term of the divisor:
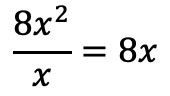
We put the result in the quotient:

As before, we multiply the new term of the quotient by each element of the divisor and put the results in the dividend:
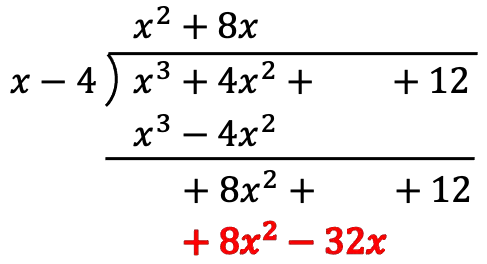
And we subtract the like terms:

The polynomial of the dividend does not yet have a lower degree than the polynomial of the divisor, so we must continue doing the same process.
So first we divide the first term of the dividend by the first term of the divisor, secondly we multiply the result by each term of the divisor, then we put the results into the dividend, and finally we subtract vertically:
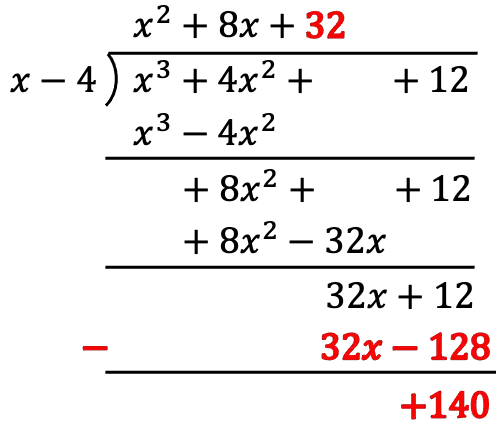
Now we can’t bring down any other term from the dividend, so the polynomial division is done. Thus, the answer of the division of these two polynomials is the quotient plus the remainder divided by the divisor:
Properties of the division of polynomials
The division of polynomials has the following characteristics:
✓ The degree of the dividend polynomial must always be greater than the degree of the divisor polynomial.
✓ The degree of the dividend polynomial equals to the sum of the degrees of the divisor and the quotient.
✓ The degree of the remainder is always less than the degree of the divisor (and therefore also of the dividend).
✓ The dividend is equal to the divisor times the quotient plus the remainder. This condition is also met in the division of numbers.
Practice problems on dividing polynomials
Problem 1
Find the following division of two polynomials:
To perform the division of polynomials we must apply the method explained above:
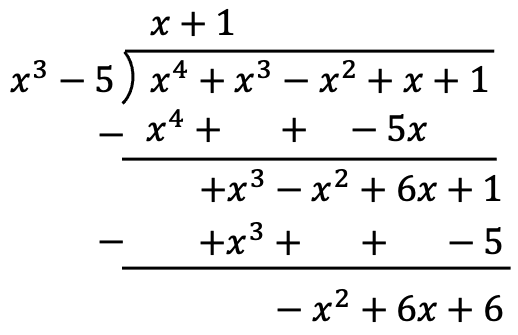
So the result of the division of the two polynomials is:
Problem 2
Calculate the following division of polynomials:
To solve the division of the polynomial by the binomial we will use the polynomial long division method:
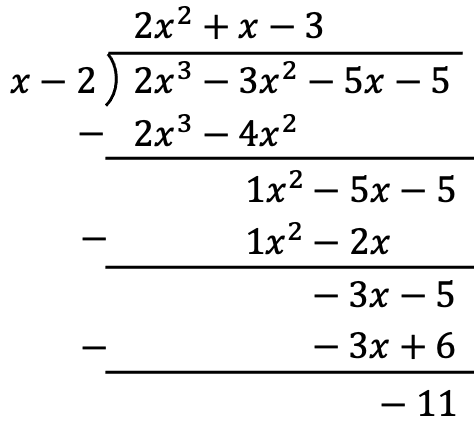
So the result of the polynomial division is:
Problem 3
Divide the following two polynomials:
To calculate the division of polynomials we must apply the explained method:
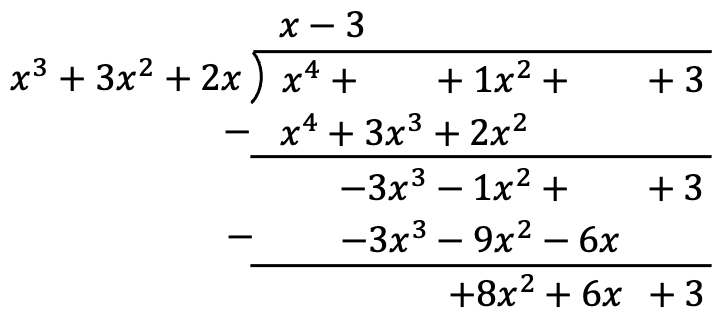
So the result of the division of the two polynomials is:
Problem 4
Solve the following division of a polynomial by a polynomial:
To compute the division of the polynomial by the trinomial we must apply the polynomial long division algorithm:
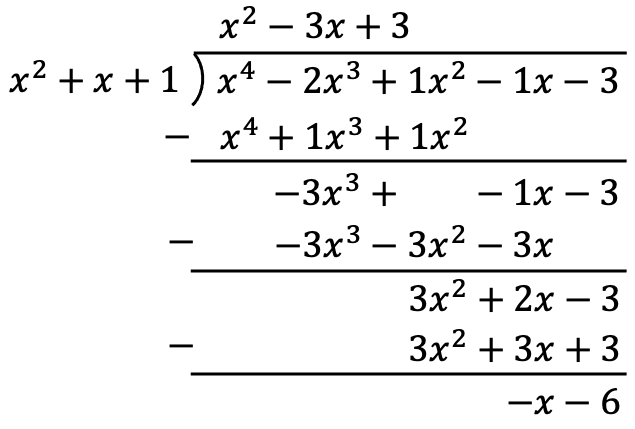
So the result of the division between the two polynomials is: