- How to multiply matrices? - When can't 2 matrices be multiplied?

On this post you will see how to calculate a matrix multiplication. We explain the procedure of multiplying matrices step by step through an example, and then you will find solved exercises so that you can also practice. Finally, you will learn when two matrices cannot be multiplied and all the properties of this matrix operation.

Table of Contents

How to multiply two matrices?

To multiply two matrices, multiply the rows of the matrix on the left by the columns of the matrix on the right.

Let’s see the procedure of how to do the multiplication of two matrices with an example:

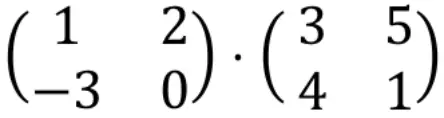
First of all, we have to multiply the first row of the matrix on the left by the first column of the matrix on the right. To do this, we multiply each element in the first row by each element in the first column one by one, and then we add the results. So all of this will be the first element in the first row of the resulting matrix. Take a look at the procedure:

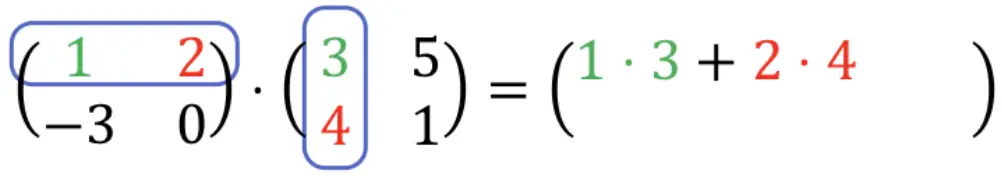
We do the calculations:

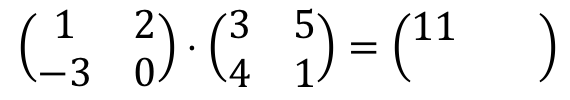
Secondly, we have to multiply the first row by the second column. So we repeat the procedure: we multiply each element in the first row by each element in the second column one by one, and then we add the results. And all this will be the second element of the first row of the resulting matrix:

We perform the operations:

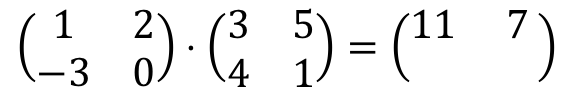
Once we have calculated the first row of the resulting matrix, we move on to the second row. So we multiply the second row by the first column repeating the procedure: we multiply each element of the second row by each element of the first column one by one, and then we add the results:

Thus:

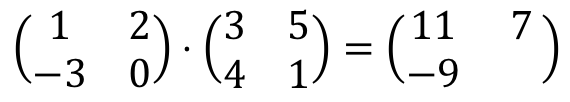
how to calculate a matrix multiplication

Finally, we multiply the second row by the second column. Always applying the same procedure: we multiply each element in the second row by each element in the second column one by one, and then we add the results:

Which results in the following matrix:

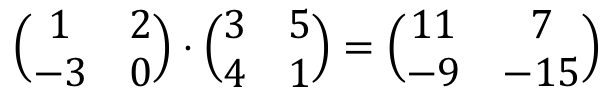
And here ends the product of the two matrices. As you have seen, the rows have to be multiplied by the columns, always repeating the same procedure: we multiply each element in the row by each element in the column one by one, and then we add the results of the multiplications.

Practice matrix multiplication

Problem 1

Solve the following 2×2 matrix multiplication:

See solution

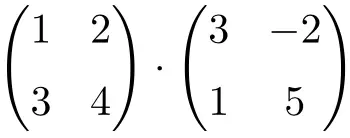
It is a product of matrices of order 2:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

To solve a matrix product we must multiply the rows of the matrix on the left by the columns of the matrix on the right.

Therefore, we first multiply the first row by the first column. To do this, we multiply each element in the first row by each element in the first column one by one, and add the results.

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Now we multiply the first row by the second column in order to find the second element of the first row of the resulting matrix:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

We go to the second row, so we multiply the second row by the first column:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Finally, we multiply the second row by the second column to calculate the last element of the matrix:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

So the result of the matrix product of 2×2 matrices is as follows:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Problem 2

Multiply the following 2×2 matrices:

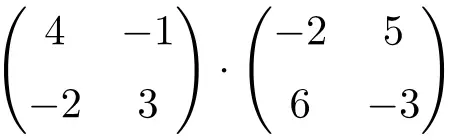
example of multiplying matrices of order 2

See solution

To solve the matrix product we have to multiply the rows of the matrix on the left by the columns of the matrix on the right:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Problem 3

Calculate the following 3×3 matrix multiplication:

See solution

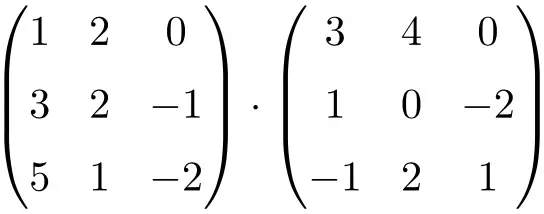
To perform the 3×3 matrix multiplication, we must multiply the rows of the matrix on the left by the columns of the matrix on the right:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Problem 4

Given matrix A:

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Calculate:

$\displaystyle 2A\cdot A^T$

See solution

First we will calculate the transpose of matrix A in order to do the multiplication. And to transpose a matrix we have to interchange its rows by its columns, in other words, the first row of the matrix becomes the first column of the matrix, and the second row of the matrix becomes the second column of the matrix.

$\displaystyle A^T= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

So the matrix operation is:

$\displaystyle 2A\cdot A^T = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Now we can do the calculations. We first multiply matrix A by the scalar 2 (although we could also calculate A·A^T first):

$\displaystyle =\begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

And finally, we solve the matrix product:

$\displaystyle =\begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Problem 5

Given the following matrices:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Calculate:

$\displaystyle A\cdot B - B \cdot A$

See solution

It is an operation that combines a subtraction together with a multiplication of square matrices of order 2:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

We first calculate the multiplication on the left:

$\displaystyle =\begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}=$

Now we solve the multiplication on the right:

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix} =$

And finally we subtract the matrices:

$\displaystyle =\begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

When can’t two matrices be multiplied?

Due to the matrix multiplication rules, not all matrices can be multiplied. Two matrices can only be multiplied if the number of columns of the matrix on the left is the same as the number of rows of the matrix on the right.

For example, the following multiplication cannot be performed because the first matrix has 3 columns and the second matrix has 2 rows:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

However, if we reverse the order, they can be multiplied. Since the first matrix has two columns and the second matrix has two rows:

$\displaystyle\begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix}$

Properties of matrix multiplication

This type of matrix operation has the following characteristics:

Matrix multiplication is associative, so the following equation always holds:

$\displaystyle\left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

Matrix multiplication also has the distributive property, so:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

The product of matrices is not commutative, that is, the result of multiplying two matrices depends on the order in which they are multiplied:

$\displaystyle A \cdot B \neq B \cdot A$

For example, the following matrix multiplication gives a result:

$\displaystyle\begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix}=\begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}$

But the result of the product is different if we change the order of matrix multiplication:

$\displaystyle\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}$

When the multiplication of two matrices gives the same result regardless of the multiplication order $(AB=BA),$ they are commuting matrices. But these type of matrices are very unusual.

Multiplying two matrices and then transposing the result is equivalent to transposing each matrix first and then multiplying them but changing their order of multiplication:

$\left(A\cdot B\right)^T=B^T\cdot A^T$

Also, any matrix multiplied by the identity matrix results in the same matrix. This is called the multiplicative identity property:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

For example:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Any matrix multiplied by the null matrix is equal to the null matrix. This is called the multiplicative property of zero:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

For example:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

How to multiply two matrices?

Practice matrix multiplication

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

When can’t two matrices be multiplied?

Properties of matrix multiplication

Leave a Comment Cancel Reply