Adding polynomials

On this post you will find the explanation of how to do the addition of polynomials. Also, you will see examples of sums of polynomials and even exercises solved step by step. Finally, we also explain what are the properties of this type of operation with polynomials.

How to add polynomials

To add two or more polynomials, add the terms of the polynomials that are like terms. That is, the addition of polynomials consists of adding the terms that have the same variables and the same exponents.

Thus, an addition of polynomials can be done with two different methods: the horizontal method or the vertical method. Here is an explanation of both procedures.

Horizontal addition of polynomials

Let’s see how to do an addition of polynomials with the horizontal method solving an example:

• Find the sum of the following two polynomials:

First of all, we have to place the two polynomials in the same operation, in other words, one polynomial after another:

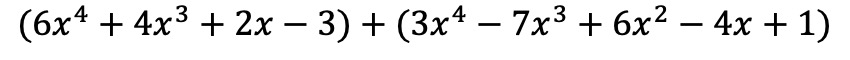
And now we add the terms that have the same variables (letters) with the same exponents. Terms that are not like terms cannot be added.

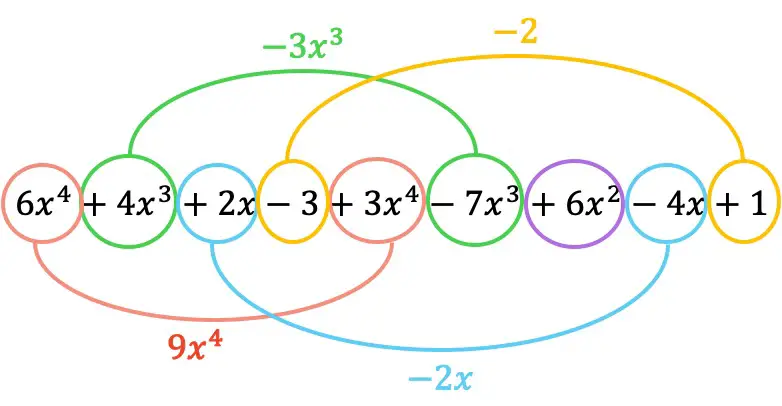
So the result of the addition of polynomials is:

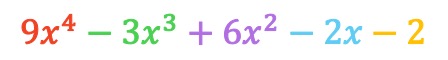
Vertical addition of polynomials

We have just seen how to add polynomials horizontally, but now we are going to see the other method that there is to do an addition of polynomials: adding polynomials vertically. And so that you can see the differences between the two methods, we will add the same polynomials as in the previous example:

• Add the following two polynomials:

The first thing we must do is place one polynomial below another, so that the like terms of the two polynomials are aligned by columns:

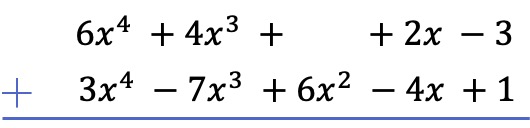
Note: if a polynomial does not have a term of a certain degree, we must leave a blank space. For example, the polynomial does not have a monomial of second degree, so there is a blank space in its place.

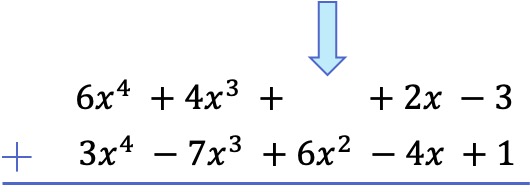
Once we have arranged all the terms from highest to lowest degree, we add the coefficients of each column, keeping the variables and exponents the same:

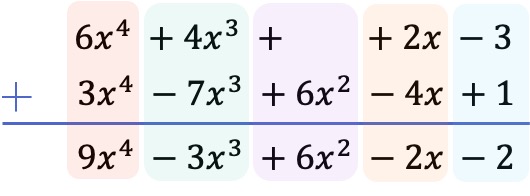
Therefore, the result obtained from the addition of the 2 polynomials is:

As you can see, we have obtained the same result with both methods, so when you do an addition of polynomials you can use the method you prefer.

Practice problems on adding polynomials

We leave you with several practice problems of additions of polynomials. If you have any questions, you can ask them below in the comments.

Problem 1

Add the following two polynomials:

In this case, we will add the two polynomials vertically. To do this, we order the polynomials by degree and add the terms in the same column:

 

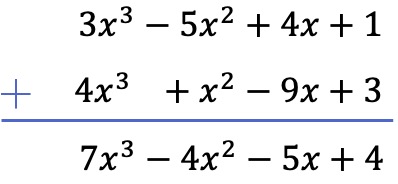
Problem 2

Solve the addition of the following two polynomials:

We will do the sum of the two polynomials using the vertical method. So we order the polynomials by degree and add the terms in the same column:

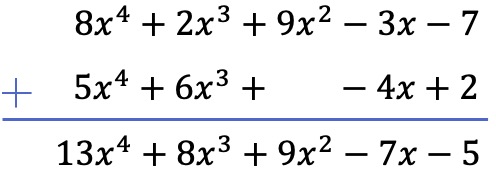
Note that in this particular case we must leave an empty space in the second degree column of the second polynomial, because it does not have a second degree term.

 

Problem 3

Simplify the following addition of two polynomials:

We will add the two polynomials using the vertical method. Therefore:

 

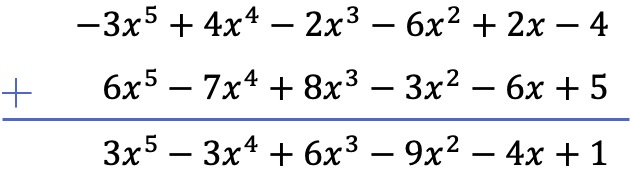
Problem 4

Add the following three polynomials:

We will calculate the addition of the 3 polynomials using the vertical method. So we put the polynomials ordered by degree and add the terms that are in the same column:

 

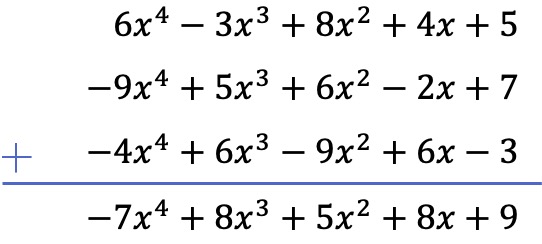
Properties of the addition of polynomials

The addition of polynomials has the following characteristics:

• Associative property: when 3 or more polynomials are added, it does not matter how the polynomials are grouped, since the result is always the same. That is, the following equation is true:

• Commutative property: in the sum of polynomials the order of the addends does not alter the result of the sum.

• Neutral element: logically, adding a polynomial plus the zero polynomial is equivalent to the first polynomial.

• Opposite element: the result of adding any polynomial plus its opposite polynomial is always null.