▷ Determinant of a 2x2 matrix - Algebra practice problems ✅

On this post we explain you what the determinant of a 2×2 matrix is and how to find the determinant of a 2×2 matrix. In addition, you will find examples and exercises solved step by step on how to solve determinants of order 2, so that you can practice and understand perfectly how to do it.

Table of Contents

What is a 2×2 determinant?

A determinant of order 2 is a 2×2 dimension matrix represented with a vertical bar on each side of the matrix. For example, if we have the following matrix:

$\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}$

The determinant of matrix A is represented as follows:

$\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}$

As you have seen, writing the determinant of a 2×2 square matrix is easy. Now let’s see how to calculate the determinant of a 2×2 matrix with its formula.

How to find the determinant of a 2×2 matrix?

To calculate the determinant of a 2×2 matrix, multiply the elements of the 2×2 matrix on the main diagonal and subtract the product of the elements on the secondary diagonal.

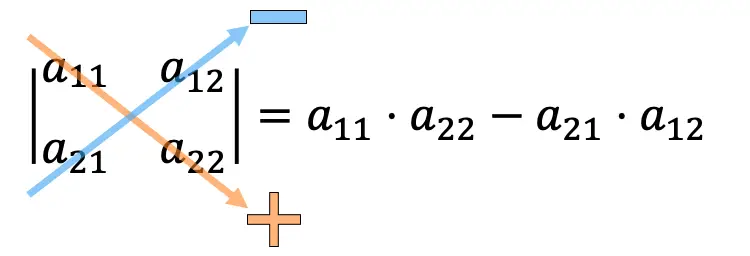
how to find the determinant of a 2x2 matrix

Examples of determinants of 2×2 matrices:

You can see the process to calculate 2×2 determinants in the following examples:

$\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}$

$\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}$

Note that the determinant of a matrix can only be calculated if the matrix is square.

Now that you have seen how to compute the determinant of a 2×2 matrix, you should see how to find the determinant of a 3×3 matrix.

Practice determinants of 2×2 matrices

Problem 1

Calculate the determinant of the following 2×2 matrix:

See solution

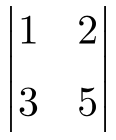
To solve the determinant of a 2×2 matrix we have to multiply the elements on the main diagonal and subtract the product of the secondary diagonal:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}$

Problem 2

Solve the determinant of the following 2×2 dimension matrix:

See solution

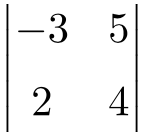
To find the solution of a determinant of order 2 we must multiply the elements of the matrix on the main diagonal and subtract the product of the secondary diagonal:

$\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}$

Problem 3

Find the determinant of the following 2×2 matrix:

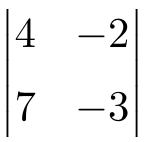
how to get the determinant of a 2x2 matrix

See solution

To find the determinant of a 2×2 square matrix, we must first multiply the elements on the main diagonal and then subtract the product of the secondary diagonal:

$\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}$

Problem 4

Take the determinant of the following 2×2 matrix:

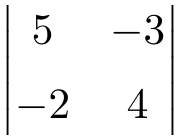
how to evaluate the determinant of a 2x2 matrix

See solution

To calculate determinants of 2×2 matrices we have to multiply the elements on the main diagonal and subtract the product of the secondary diagonal, so:

$\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}$

Problem 5

Determine the result of the following 2×2 determinant:

See solution

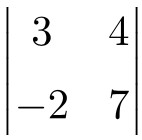
To find the solution of a 2-by-2 determinant we simply have to multiply the elements on the main diagonal and subtract the product of the secondary diagonal:

$\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}$

Problem 6

Find the value of x in the following 2×2 matrix if its determinant equals to 8:

$\displaystyle \begin{vmatrix}-2&x\\[1.1ex]-4&6\end{vmatrix}$

See solution

First we get the determinant of the matrix by applying the formula:

$\displaystyle \begin{vmatrix}-2&x\\[1.1ex]-4&6\end{vmatrix}=-2\cdot 6-(-4)\cdot x=-12+4x$

The problem says that the determinant results in 8, thus, we have to set the expression obtained equal to 8:

$-12+4x=8$

And we solve the linear equation to find the value of x:

$-12+4x+12=8+12$

$4x=20$

$\cfrac{4x}{4}=\cfrac{20}{4}$

$\bm{x=5}$

Did you know that 2×2 determinants are used to solve systems of linear equations? To do this, we use Cramer’s rule 2×2.

Can the determinant of a 2×2 matrix be zero?

The determinant of a 2×2 matrix can be equal to zero, for example:

$\displaystyle \begin{vmatrix}3&2\\[1.1ex]9&6\end{vmatrix}=3\cdot 6-2\cdot9=18-18=0$

However, the result of the determinant indicates the invertibility of the matrix:

If the determinant of a 2×2 matrix is zero, such matrix is a non-invertible matrix.
If the determinant of a 2×2 matrix is nonzero, such matrix is invertible (non-singular matrix).

Therefore, it is very important whether the determinant of a matrix of order 2 is 0 or not, since it will be a type of matrix or another.

Determinant of a 2×2 matrix

What is a 2×2 determinant?

How to find the determinant of a 2×2 matrix?

Examples of determinants of 2×2 matrices:

Practice determinants of 2×2 matrices

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Can the determinant of a 2×2 matrix be zero?

2 thoughts on “Determinant of a 2×2 matrix”

Leave a Comment Cancel Reply