How to solve systems of equations using Cramer's rule (practice)

On this post we explain what Cramer’s rule is and, in addition, you will find examples and exercises of systems of equations solved by Cramer’s rule.

Table of Contents

Cramer’s rule formula

Cramer’s rule is a formula used to solve systems of linear equations using determinants. Let’s see how to use the Cramer’s rule:

Given a system of linear equations:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

Let A be a square matrix with the coefficients of the unknowns:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right)$

Cramer’s rule states that the solution of a system of equations can be computed as follows:

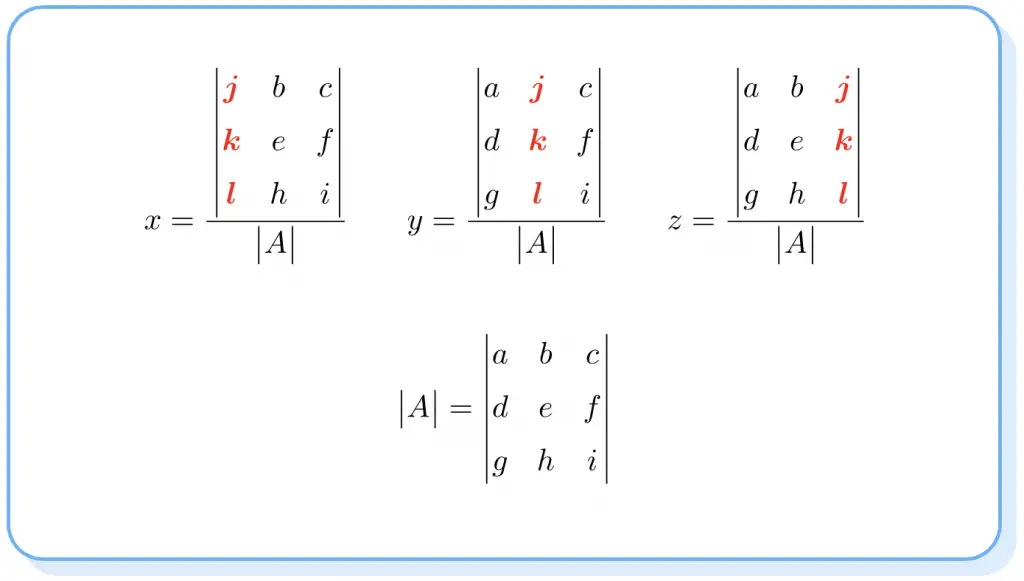
Note that the determinants of the numerators are like the determinant of matrix A but changing the column of each unknown by the column of the constants. And the determinant of the denominator of the fraction is always the determinant of matrix A.

Therefore, Cramer’s method is used to solve systems of linear equations. But there are many other ways to solve a system of equations, for example the Gaussian elimination method.

Below you can see an example of how to solve a system of linear equations using Cramer’s rule.

Cramer’s rule example

Solve the following system of 3 equations with 3 unknowns using Cramer’s rule:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

First of all, we construct matrix A with the coefficients of the unknowns:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right)$

Now we apply the Cramer’s rule to solve the system of equations. To do this, we first have to find the determinant of matrix A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

To calculate the unknown x with Cramer’s rule, we replace the first column of the determinant of A by the column of constants and divide it by the determinant of A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

To find the unknown y with Cramer’s rule, we change the second column of the determinant of A for the column of constants and divide it by the determinant of A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

And finally, to compute variable z with Cramer’s rule we interchange the third column of the determinant of A with the column of constants and divide it by the determinant of matrix A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

Therefore, the solution of the system of linear equations is:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

Practice problems of Cramer’s rule

Problem 1

Apply Cramer’s rule to solve the following system of two equations with 2 unknowns:

See solution

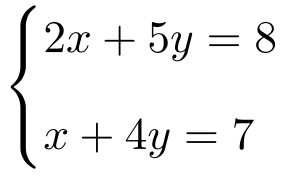
First we construct matrix A with the coefficients of the variables:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right)$

Now we use the Cramer’s rule to solve the system of equation. So we evaluate the determinant of matrix A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3$

To calculate the unknown x with Cramer’s rule, we change the first column of the determinant of A for the column of constants and divide it by the determinant of A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

And to find the value of the unknown y, we change the second column of the determinant of A for the column of contants and divide it by the determinant of matrix A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

Thus, the solution of the system of equations is:

$\displaystyle \bm{x = -1 \qquad y=2}$

Problem 2

Find the solution of the following system of three equations with 3 unknowns using Cramer’s rule:

See solution

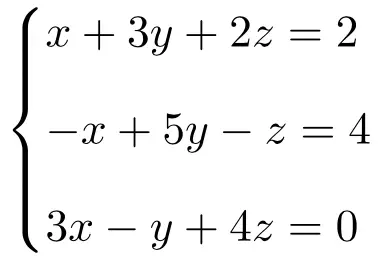
Matrix A is the matrix with all the coefficients of the variables:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right)$

We calculate the determinant of matrix A to apply Cramer’s rule:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix}=-6$

To calculate the unknown x using Cramer’s method, we change the first column of the determinant of A for the column of constants and divide it by the determinant of A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

Secondly, to find the unknown y with Cramer’s method, we replace the second column of the determinant of A by the column of constants and divide it by the determinant of A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

And finally, to compute z with Cramer’s rule, we change the third column of the determinant of A for the column of constants and divide it by the determinant of A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

Thus, the solution of the system of equations is:

$\displaystyle\bm{x =3 \qquad y=1 \qquad z=-2}$

Problem 3

Solve the following system of linear equations applying Cramer’s rule:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

See solution

First, we find matrix A of the system:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right)$

Now we use Cramer’s rule to solve the system. First we take the determinant of matrix A:

$\displaystyle\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix}=-8$

To calculate the unknown x with Cramer’s rule, we change the first column of the determinant of A for the column of constants and divide it by the determinant of A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

To find the unknown y using Cramer’s rule, we interchange the second column of the determinant of A with the column of constants and divide it by the determinant of A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

To compute the unknown z with Cramer’s rule, we replace the third column of the determinant of A by the column of constants and divide it by the determinant of A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

So the solution of the system of linear equations is:

$\displaystyle\bm{x =-2 \qquad y=0 \qquad z=4}$

Cramer’s rule formula

Cramer’s rule example

Practice problems of Cramer’s rule

Problem 1

Problem 2

Problem 3

Leave a Comment Cancel Reply