How to find the Determinant of a 3x3 Matrix (practice problems)

Here we explain how to find the determinant of a 3×3 matrix using the cofactor expansion method or using the shortcut method. Also, you will see examples of the computations of 3×3 determinants and, finally, you will find solved exercises so that you can practice and perfectly understand how to evaluate the determinant of a 3×3 matrix.

Table of Contents

What is the determinant of a 3×3 matrix?

The determinant of a 3×3 matrix is a matrix of order 3 represented with a vertical bar on each side of the matrix. For example, if we have the following matrix:

$\displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}$

The determinant of square matrix A is represented as follows:

$\displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}$

As you have seen, writing determinants of 3×3 matrices is simple. Now let’s see how to solve them:

Determinant of a 3×3 matrix: cofactor expansion

To find the determinant of a 3×3 dimension matrix:

Multiply the element a by the determinant of the 2×2 matrix obtained by eliminating the row and column where a is located.
Repeat the procedure for elements b and c.
Add the product of elements a and c, and subtract the product of element b.

Thus, the calculation of the determinant of a 3×3 matrix is decomposed into 2×2 determinants. So the formula to compute the determinant of a 3×3 matrix is as follows:

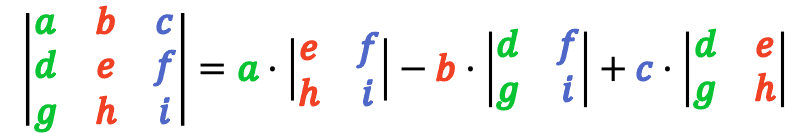
This method to calculate the determinant of a 3×3 matrix is called the cofactor expansion method.

Remember that to find the determinant of a 2×2 matrix, you have to multiply the elements on the main diagonal and subtract the product of the elements on the secondary diagonal.

Example of the determinant of a 3×3 matrix

Once we’ve seen the formula to find the determinant of a 3×3 matrix, let’s see an example of how to do the calculation:

$\begin{aligned}\begin{vmatrix}1&3&-2\\[1.1ex]0&5&1\\[1.1ex]4&-1&2\end{vmatrix}& =1\cdot \begin{vmatrix}5&1\\[1.1ex]-1&2\end{vmatrix}-3\cdot \begin{vmatrix}0&1\\[1.1ex]4&-2\end{vmatrix}+(-2)\cdot \begin{vmatrix}0&5\\[1.1ex]4&-1\end{vmatrix}\\ &=1\cdot \Bigl[10-(-1)\Bigr]-3\cdot\Bigl[0-4\Bigr]-2\cdot\Bigl[0-20\Bigr]\\[2ex]&= 1\cdot11-3\cdot(-4)-2\cdot(-20)\\[2ex]&=11+12+40\\[2ex]&=63 \end{aligned}$

Determinant of a 3×3 matrix: shortcut method

There is another method to evaluate the determinant of a 3×3 matrix called the shortcut method, whose rules are:

Duplicate the first two columns of the matrix to the right of its third column.
Add the products of the main diagonals going from top to bottom.
Subtract the products of the main diagonals going from bottom to top.

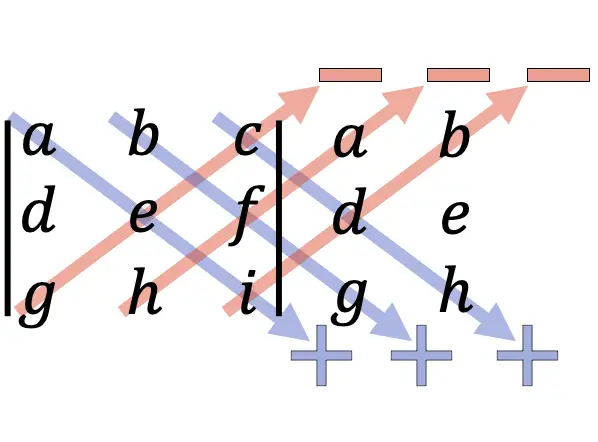
rule of sarrus for computing the determinant of a 3x3 matrix

This method is an easy way to find the determinant of a 3×3 matrix using its diagonals. Moreover, this method is also known as Rule of Sarrus or Scheme of Sarrus.

You can see how to apply the shortcut method in the following example:

$\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

First we rewrite the first two columns to the right of the 3×3 matrix:

$\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \ \begin{matrix}2 & 1\\[1.1ex] -1 & 1\\[1.1ex] -2 & 4\end{matrix}$

And then we add the products of the main diagonals going from top to bottom and subtract the products of the main diagonals going from bottom to top:

$\begin{aligned}\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \ \begin{matrix}2 & 1\\[1.1ex] -1 & 1\\[1.1ex] -2 & 4 \end{matrix} \ & = \begin{array}{l}\\[2ex]2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + 3\cdot (-1) \cdot 4 \\[2ex] - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- 1\cdot (-1) \cdot 1\end{array} \\[2ex] & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & =-3 \end{aligned}$

Practice problems on finding the determinant of a 3×3 matrix

Problem 1

Find the determinant of the following 3×3 matrix:

$\begin{vmatrix}5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0\end{vmatrix}$

See solution

We can solve the determinant of the 3×3 matrix using the formula:

$\begin{aligned}\begin{vmatrix}5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0\end{vmatrix}& =5\cdot \begin{vmatrix}3&4\\[1.1ex]1&0\end{vmatrix}-0\cdot \begin{vmatrix}1&4\\[1.1ex]-1&0\end{vmatrix}+2\cdot \begin{vmatrix}1&3\\[1.1ex]-1&1\end{vmatrix}\\ &=5\cdot \Bigl[0-4\Bigr]-0\cdot\Bigl[0-(-4)\Bigr]+2\cdot\Bigl[1-(-3)\Bigr]\\[2ex]&= 5\cdot(-4)-0+2\cdot4\\[2ex]&=-20+8\\[2ex]&=\bm{-12} \end{aligned}$

This 3×3 determinant was easy to compute since there is a zero in the first row of the matrix.

The determinant can also be computed using the shortcut method. We duplicate the first two columns of the matrix to its right:

$\begin{vmatrix} 5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0\end{vmatrix} \ \begin{matrix}5&0\\[1.1ex]1&3\\[1.1ex]-1&1\end{matrix}$

And then we apply the Sarrus’ rule:

$\begin{aligned}\begin{vmatrix} 5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0 \end{vmatrix} \ \begin{matrix}5&0\\[1.1ex]1&3\\[1.1ex]-1&1\end{matrix} \ & = \begin{array}{l}\\[2ex]5 \cdot 3 \cdot 0 + 0 \cdot 4 \cdot (-1) + 2 \cdot 1 \cdot 1 \\[2ex] - (-1) \cdot 3 \cdot 2 - 1 \cdot 4 \cdot 5- 0 \cdot 1 \cdot 0 \end{array} \\[2ex] & =0+0+2+6-20+0\\[2ex] & =\bm{-12} \end{aligned}$

Problem 2

Compute the determinant of the following matrix of order 3:

$\begin{vmatrix}1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix}$

See solution

To find the 3×3 determinant we can use the general method:

$\begin{aligned}\begin{vmatrix}1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix}& =1\cdot \begin{vmatrix}1&4\\[1.1ex]-3&2\end{vmatrix}-3\cdot \begin{vmatrix}5&4\\[1.1ex]2&2\end{vmatrix}+(-2)\cdot \begin{vmatrix}5&1\\[1.1ex]2&-3\end{vmatrix}\\ &=1\cdot \Bigl[2-(-12)\Bigr]-3\cdot\Bigl[10-8\Bigr]-2\cdot\Bigl[-15-2\Bigr]\\[2ex]&= 1\cdot14-3\cdot2-2\cdot(-17)\\[2ex]&=14-6+34\\[2ex]&=\bm{42} \end{aligned}$

On the other hand, the determinant can also be found using the shortcut method. First we rewrite the first two columns of the matrix to its right:

$\begin{vmatrix} 1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix} \ \begin{matrix}1&3\\[1.1ex]5&1\\[1.1ex]2&-3\end{matrix}$

And then we apply the Sarrus’ formula:

$\begin{aligned}\begin{vmatrix}1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix} \ \begin{matrix}1&3\\[1.1ex]5&1\\[1.1ex]2&-3\end{matrix} \ & = \begin{array}{l}\\[2ex]1 \cdot 1 \cdot 2 + 3 \cdot 4 \cdot 2 + (-2) \cdot 5 \cdot (-3) \\[2ex] - 2 \cdot 1 \cdot (-2) - (-3) \cdot 4 \cdot 1- 2 \cdot 5\cdot 3 \end{array} \\[2ex] & =2+24+30+4+12-30\\[2ex] & =\bm{42} \end{aligned}$

Problem 3

Evaluate the determinant of the following 3×3 square matrix:

$\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix}$

See solution

To evaluate the 3×3 determinant we can apply the standard formula:

$\begin{aligned}\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix}& =4\cdot \begin{vmatrix}6&1\\[1.1ex]2&-4\end{vmatrix}-1\cdot \begin{vmatrix}-2&1\\[1.1ex]3&-4\end{vmatrix}+5\cdot \begin{vmatrix}-2&6\\[1.1ex]3&2\end{vmatrix}\\ &=4\cdot \Bigl[-24-2\Bigr]-1\cdot\Bigl[8-3\Bigr]+5\cdot\Bigl[-4-18\Bigr]\\[2ex]&= 4\cdot(-26)-1\cdot5+5\cdot(-22)\\[2ex]&=-104-5-110\\[2ex]&=\bm{-219} \end{aligned}$

Or we can also calculate the 3×3 determinant using the diagonals method. To do so, we duplicate the first two columns of the matrix to its right:

$\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix} \ \begin{matrix}4&1\\[1.1ex]-2&6\\[1.1ex]3&2\end{matrix}$

And finally we use the Sarrus’ scheme to solve the 3-by-3 determinant:

$\begin{aligned}\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix} \ \begin{matrix}4&1\\[1.1ex]-2&6\\[1.1ex]3&2\end{matrix} \ & = \begin{array}{l}\\[2ex]4\cdot 6 \cdot (-4) + 1 \cdot 1 \cdot 3 + 5 \cdot (-2) \cdot 2 \\[2ex] - 3 \cdot 6 \cdot 5 - 2 \cdot 1 \cdot 4- (-4) \cdot (-2)\cdot 1 \end{array} \\[2ex] & =-96+3-20-90-8-8=\\[2ex] & =\bm{-219} \end{aligned}$

Problem 4

Find the value of x in the following 3×3 matrix that makes its determinant equal to 0:

$\displaystyle \begin{pmatrix}4&6&-5\\[1.1ex]-2&4&2\\[1.1ex]-1&2&x\end{pmatrix}$

See solution

First we get the determinant of the matrix by applying the general formula or the shortcut method:

$\begin{aligned}\begin{vmatrix}4&6&-5\\[1.1ex]-2&4&2\\[1.1ex]-1&2&x\end{vmatrix}& =4\cdot \begin{vmatrix}4&2\\[1.1ex]2&x\end{vmatrix}-6\cdot \begin{vmatrix}-2&2\\[1.1ex]-1&x\end{vmatrix}+(-5)\cdot \begin{vmatrix}-2&4\\[1.1ex]-1&2\end{vmatrix}\\ &=4\cdot \Bigl[4x-4\Bigr]-6\cdot\Bigl[-2x+2\Bigr]-5\cdot\Bigl[-4+4\Bigr]\\[2ex]&= 16x-16+12x-12+0\\[2ex]&=28x-28\end{aligned}$