What is a Singular (or Degenerate) matrix? (examples)

On this post you will find what a singular (or degenerate) matrix is and when a matrix is singular. We also show you several examples of singular matrices and, finally, we explain all the properties of this type of matrix.

Table of Contents

What is a singular matrix?

The definition of a singular matrix, also known as a degenerate matrix, is as follows:

A singular (or degenerate) matrix is a square matrix whose inverse matrix cannot be calculated. Therefore, the determinant of a singular matrix is equal to 0.

When is a matrix singular?

You have to solve the determinant of the matrix to know when a matrix is singular:

If the determinant of the matrix is equal to zero, the matrix is singular or non-invertible.
If the determinant of the matrix is nonzero, the matrix is invertible.

See: invertible matrix

In conclusion, calculating the determinant of a matrix is the easiest way to check the invertibility of a matrix.

However, if you want to find the value of the inverse of a matrix, you should see how to calculate the inverse of a matrix.

Examples of singular matrices

Having seen the meaning of singular or degenerate matrix, let’s see some examples of singular matrices of different dimensions:

Example of a 2×2 singular matrix

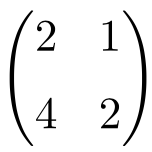
example of 2x2 dimension singular matrix

We can easily check that it is a singular matrix by calculating its determinant:

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 4 & 2 \end{vmatrix} \bm{= 0}$

The solution of the determinant of the matrix of order 2 is equal to 0, so it is a singular matrix.

Example of a 3×3 singular matrix

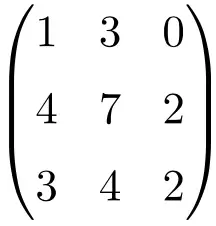
example of 3x3 dimension singular matrix

We must find the determinant of the matrix to prove that it is a non-invertible matrix:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

The determinant of the matrix of order 3 results in 0, therefore, it is a singular matrix.

Example of a 4×4 singular matrix

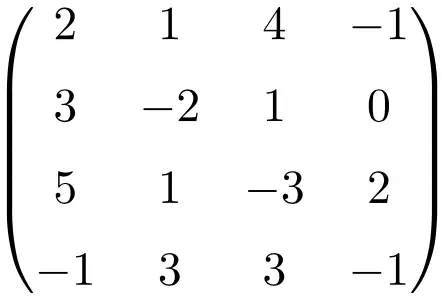
By calculating the determinant of the matrix it is proven that it is a singular matrix:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

The determinant of the matrix of order 4 is null, so its inverse matrix does not exist.

If you have questions about the calculations of the determinants, you can consult how to calculate a determinant in our website.

Properties of singular matrices

The characteristics of singular matrices are the following:

At least two columns or two rows of a singular matrix are linear combination and are therefore linearly dependent.

Any matrix that contains a row or column filled with zeros is a singular matrix.

The rank of a singular or degenerate matrix is less than its size.

The matrix product of a singular matrix multiplied by any other matrix results in another singular matrix. This condition can be deduced from the properties of the determinants:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Similarly, the power of a singular matrix is equal to another singular matrix, regardless of the exponent to which it is raised.

The transpose of a singular matrix gives another singular matrix, since the determinant of a transposed matrix is equivalent to the determinant of the untransposed matrix:

$\text{det}(A^T) = \text{det}(A)=0$

Multiplying a singular matrix by a scalar does not change its condition as a degenerate matrix.

The adjoint of a singular matrix is also singular.

See: how to find the adjoint of a matrix.

Triangular matrices and diagonal matrices are degenerate matrices if at least one element of their main diagonal is zero.

Obviously, the null matrix is a singular matrix.

In the same way, a nilpotent matrix is also a singular matrix.

A system of linear equations associated with a singular matrix has no solution or has infinite solutions.

Finally, a square matrix is singular if and only if it has at least one eigenvalue equal to 0.

Singular (or degenerate) matrix