What is an Invertible matrix? - And when is a matrix Invertible?

On this post you will find what an invertible is and how to know when a matrix is invertible. In addition, you will also see several examples of invertible matrices to perfectly understand the concept and, finally, we will show you the invertible matrix theorem and all the properties of this type of matrices.

Table of Contents

What does invertible matrix mean?

The definition of invertible matrix is as follows:

An invertible matrix is a square matrix whose inverse matrix can be calculated, that is, the product of an invertible matrix and its inverse equals to the identity matrix. The determinant of an invertible matrix is nonzero.

Invertible matrices are also called non-singular or non-degenerate matrices.

On the other hand, the singular or degenerate matrix is the opposite matrix to the invertible matrix, so a singular matrix is non-invertible.

When is a matrix invertible?

You have to solve the determinant of the matrix to know when a matrix is invertible or not:

If the determinant of the matrix is nonzero, the matrix is invertible.
If the determinant of the matrix is equal to zero, the matrix is non-invertible.

In conclusion, calculating the determinant of a matrix is the fastest way to know whether the matrix has an inverse or not, so it is what we recommend to determine the invertibility of any type of matrix.

But this does not work to perform the inversion of the matrix. If you want to know how a matrix is inverted, you can see the formula for the inverse of a matrix here, you will also find several examples and exercises with answers to practice.

Examples of invertible matrices

Once we have seen the meaning of invertible matrix, let’s see some examples of invertible matrices of different dimensions:

Example of a 2×2 invertible matrix

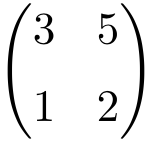
We can prove that it is an invertible matrix by calculating its determinant:

$\displaystyle \begin{vmatrix} 3 & 5 \\[1.1ex] 1 & 2 \end{vmatrix} = 1 \bm {\neq 0}$

The determinant of the matrix of order 2 is different from 0, so it is an invertible matrix.

Example of a 3×3 invertible matrix

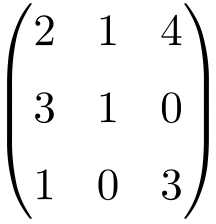
example of invertible matrix of dimension 3x3

We must find the determinant of the matrix to check that it is an invertible matrix:

$\begin{vmatrix} 2 & 1 & 4 \\[1.1ex] 3 & 1 & 0 \\[1.1ex] 1 & 0 & 3 \end{vmatrix} = - 7 \bm {\neq 0}$

The determinant of the matrix of order 3 gives as a result different from 0, therefore, it is an invertible matrix.

Example of a 4×4 invertible matrix

example of invertible matrix of dimension 4x4

To prove that it is an invertible matrix we have to calculate the determinant of the matrix:

$\displaystyle \begin{vmatrix} 1 & 3 & -2 & 0 \\[1.1ex] 2 & -1 & 0 & 5 \\[1.1ex] 1 & 3 & 1 & 2 \\[1.1ex] 0 & -1 & 2 & 4 \end{vmatrix} = -49 \bm {\neq 0}$

The determinant of the matrix of order 4 is not null, so it is an invertible matrix.

If you have questions about the calculations of the determinants, you can consult in our page how to calculate a determinant.

Invertible matrix theorem

The invertible matrix theorem is a theorem in linear algebra which gives all the conditions that invertible matrices have.

Let A be a square nxn matrix, all the following statements are equivalent:

A is invertible, that is, A has an inverse.
The determinant of A is not zero.
A has n pivot positions.
The equation Ax=0 has only the trivial solution x=0.
A is row-equivalent to the n×n identity matrix I_n.
The columns of A form a linearly independent set.
The linear transformation mapping x to Ax is a bijection.
The linear transformation mapping x to Ax is a surjection.
For each column vector b in Rⁿ, the equation Ax=b has a unique solution.
The columns of A span Rⁿ.
There is an n×n matrix C such that CA=I_n.
There is an n×n matrix D such that AD=I_n.
The transpose matrix A^T is also invertible.
The columns of A form a basis for Rⁿ.
The column space of A is equal to Rⁿ.
The dimension of the column space of A is n.
The row space of A is Rⁿ.
The rank of A is n, so an invertible matrix has full rank.
The null space of A is {0}.
The dimension of the null space of A is 0.
0 is not an eigenvalue of matrix A.
The orthogonal complement of the column space of A is {0}.
The orthogonal complement of the null space of A is Rⁿ.
The matrix A has n non-zero singular values.

Properties of invertible matrices

Invertible matrices are very important for linear algebra, and that is due to the following characteristics:

The inverse of an inverted matrix is equal to the original matrix.

$\displaystyle \left(A^{-1} \right)^{-1} =A$

If A is an invertible matrix, so is the transpose of the matrix. Also, the inverse matrix of the transpose is equal to the transpose of the inverse.

$\displaystyle \left(A^t \right)^{-1} = \left(A^{-1} \right)^t$

The matrix product between two invertible matrices gives another invertible matrix. This condition can be easily demonstrated with the properties of the determinants:

$\displaystyle \left. \begin{array}{l} \text{det} (A \cdot B) = \text{det}(A) \cdot \text{det} (B) \\[2ex] \text{det}(A) \neq 0 \quad; \quad \text{det}(B) \neq 0 \end{array} \right\} \longrightarrow \ \text{det} (A \cdot B) \neq 0$

Any orthogonal matrix is at the same time an invertible matrix.

All eigenvalues of an invertible matrix are nonzero.