What is the complex conjugate of a matrix? (And how to find it?)

In this post we explain what a conjugate matrix is and how to find the complex conjugate of a matrix. In addition, we show you an example of the conjugate of a matrix and all the properties of this type of matrix.

Table of Contents

What is a conjugate matrix?

The definition of complex conjugate matrix is as follows.

A conjugate matrix is a complex matrix which all its elements have been replaced by their complex conjugates, that is, the sign of the imaginary part of all its complex numbers have been changed.

The conjugate matrix of $A$ is denoted with a horizontal bar above it: $\overline{A}.$

Example of the conjugate of a matrix

Once we have seen the meaning of conjugate matrix, let’s see an example to fully understand the concept:

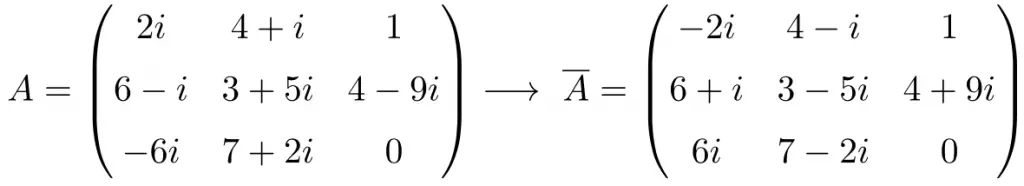
Matrix $\overline{A}$ is the conjugate of matrix A, since all entries of matrix $\overline{A}$ are conjugated. In other words, the numbers in matrix $\overline{A}$ have the same real part as numbers in matrix A, but their complex part have the opposite sign.

Properties of the conjugate matrix

The characteristics of the conjugate matrix are the following:

The conjugate of a conjugate matrix results in the original matrix.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

Adding (or subtracting) two matrices and conjugating the result is the same as first conjugating the two matrices separately and then adding (or subtracting) them.

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

See: adding and subtracting matrices.

The conjugate product of two matrices is equal to conjugating the two matrices separately and then calculating the matrix multiplication.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

See: matrix product.

Multiplying a matrix by a scalar and conjugating the result is the same as first doing the conjugates of the scalar and the matrix and then solving the product.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

See: scalar multiplication of matrices.

Transposing a matrix and then conjugating it is the same as first conjugating the matrix and then calculating its transpose.

$\displaystyle \overline{\bigl(A^T \bigr)} = \left( \overline{A}\right)^T$

See: how to transpose a matrix.

Calculating the inverse of a matrix and then its conjugate it is identical to first conjugate the matrix and later its inverse.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

The rank of a conjugate matrix is equal to the rank of the original matrix

$\displaystyle rk\left(\overline{A}\right) =rk(A)$

It is indifferent to calculate the trace of a conjugate matrix or to calculate the trace of the matrix unconjugated and then do the conjugation of the result.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

Finally, finding the determinant of a conjugate matrix equals to calculating the conjugate of the result of the determinant of the original matrix.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

Complex conjugate of a matrix

What is a conjugate matrix?

Example of the conjugate of a matrix

Properties of the conjugate matrix

Leave a Comment Cancel Reply