Hessian matrix

On this post we explain what the Hessian matrix is and how to calculate it (with examples). Also, you will find several solved exercises so that you can practice. In addition, you will see all the applications of the Hessian matrix. And finally, we will show you what the bordered Hessian matrix is.

What is the Hessian matrix?

The definition of the Hessian matrix is as follows:

The Hessian matrix, or simply Hessian, is an n×n square matrix composed of the second-order partial derivatives of a function of n variables.

The Hessian matrix was named after Ludwig Otto Hesse, a 19th century German mathematician who made very important contributions to the field of linear algebra.

Thus, the formula for the Hessian matrix is as follows:

formula of hessian matrix

Therefore, the Hessian matrix will always be a square matrix whose dimension will be equal to the number of variables of the function. For example, if the function has 3 variables, the Hessian matrix will be a 3×3 dimension matrix.

Furthermore, the Schwarz’s theorem (or Clairaut’s theorem) states that the order of differentiation does not matter, that is, first partially differentiate with respect to the variable x_1 and then with respect to the variable x_2 is the same as first partially differentiating with respect to x_2 and then with respect to x_1.

\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}

In other words, the Hessian matrix is a symmetric matrix.

Thus, the Hessian matrix is the matrix with the second-order partial derivatives of a function. On the other hand, the matrix with the first-order partial derivatives of a function is the Jacobian matrix.

Hessian matrix example

Once we have seen how to calculate the Hessian matrix, let’s see an example to fully understand the concept:

  • Calculate the Hessian matrix at the point (1,0) of the following multivariable function:

\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8

First of all, we have to compute the first order partial derivatives of the function:

\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y

\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5

Once we know the first derivatives, we calculate all the second order partial derivatives of the function:

\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6

\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8

\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4

Now we can find the Hessian matrix using the formula for 2×2 matrices:

\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}

\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}

So the Hessian matrix evaluated at the point (1,0) is:

\displaystyle H_f (1,0)=\begin{pmatrix}6\cdot 1 +6 &-4 \\[2ex] -4 & 12\cdot 0^2+8 \end{pmatrix}

\displaystyle H_f (1,0)=\begin{pmatrix}12&-4\\[2ex]-4&8\end{pmatrix}

Practice problems on finding the Hessian matrix

Problem 1

Find the Hessian matrix of the following 2 variable function at the point (1,1):

\displaystyle f(x,y)=x^2y+y^2x

First we compute the first-order partial derivatives of the function:

\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2

\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx

Then we calculate all the second-order partial derivatives of the funciton:

\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y

\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x

\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y

So the Hessian matrix is defined as follows:

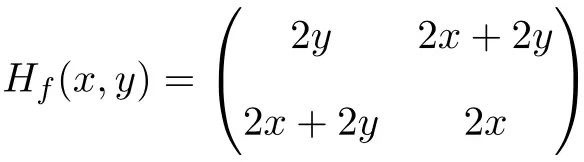
hessian matrix solved examples

Finally, we evaluate the Hessian matrix at the point (1,1):

\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}

\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}

 

Problem 2

Calculate the Hessian matrix at the point (1,1) of the following function with two variables:

\displaystyle f(x,y)= e^{y\ln x}

First we differentiate the function with respect to x and with respect to y:

\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}

\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x

Once we have the first derivatives, we calculate the second-order partial derivatives of the function:

\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}

\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x

\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}

So the Hessian matrix of the function is a square matrix of order 2:

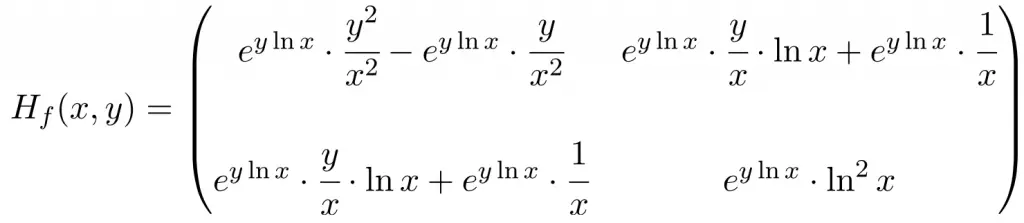
hessian matrix solved exercise

And we evaluate the Hessian matrix at the point (1,1):

\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}

\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}

\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}

\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}

 

Problem 3

Compute the Hessian matrix at the point (0,1,π) of the following 3 variable function:

\displaystyle f(x,y,z)= e^{-x}\cdot \sin(yz)

To compute the Hessian matrix first we have to calculate the first-order partial derivatives of the function:

\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \sin(yz)

\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \cos(yz)

\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \cos(yz)

Once we have computed the first derivatives, we calculate the second-order partial derivatives of the function:

\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \sin(yz)

\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \cos(yz)

\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \cos(yz)

\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \sin(yz)

\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \cos(yz)-yze^{-x}\cdot \sin(yz)

\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \sin(yz)

So the Hessian matrix of the function is a square matrix of order 3:

\displaystyle H_f(x,y,z)=\begin{pmatrix}e^{-x}\cdot \sin(xy) & -ze^{-x}\cdot \cos(yz) &-ye^{-x}\cdot \cos(yz) \\[1.5ex] -ze^{-x}\cdot \cos(yz)&-z^2e^{-x}\cdot \sin(yz) &e^{-x}\cdot \cos(yz)-yze^{-x}\cdot \sin(yz) \\[1.5ex] -ye^{-x}\cdot \cos(yz)& e^{-x}\cdot \cos(yz)-yze^{-x}\cdot \sin(yz)& -y^2e^{-x}\cdot \sin(yz)\end{pmatrix}

And finally, we substitute the variables for their respective values at the point (0,1,π):

\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \sin(1\pi) & -\pi e^{-0}\cdot \cos(1\pi) &-1e^{-0}\cdot \cos(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \cos(1 \pi)&-\pi^2e^{-0}\cdot \sin(1 \pi) &e^{-0}\cdot \cos(1 \pi)-1 \pi e^{-0}\cdot \sin(1 \pi) \\[1.5ex] -1e^{-0}\cdot \cos(1 \pi)& e^{-0}\cdot \cos(1 \pi)-1 \pi e^{-0}\cdot \sin(1 \pi)& -1^2e^{-0}\cdot \sin(1 \pi) \end{pmatrix}

\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}

\displaystyle \bm{H_f(0,1,\pi)=}\begin{pmatrix}\bm{0}&\bm{\pi}&\bm{1}\\[1.5ex]\bm{\pi}&\bm{0}&\bm{-1}\\[1.5ex]\bm{1}&\bm{-1}&\bm{0}\end{pmatrix}

 

Problem 4

Determine the Hessian matrix at the point (2, -1, 1, -1) of the following function with 4 variables:

\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2

The first step is to find the first-order partial derivatives of the function:

\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2

\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4

\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z

\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3

Now we solve the second-order partial derivatives of the function:

\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2

\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2

\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz

\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw

\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4

\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2

\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3

\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2

\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w

\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2

So the expression of the 4×4 Hessian matrix obtained by solving all the partial derivatives is the following:

4x4 hessian matrix

And finally, we substitute the unknowns for their respective values of the point (2, -1, 1, -1) and perform the calculations:

\displaystyle \bm{H_f(2,-1,1,-1)=}\begin{pmatrix}\bm{30}&\bm{-96}&\bm{48}&\bm{-48}\\[1.5ex]\bm{-96}&\bm{204}&\bm{-64}&\bm{152}\\[1.5ex]\bm{48}&\bm{-64}&\bm{24}&\bm{-32}\\[1.5ex]\bm{-48}&\bm{152}&\bm{-32}&\bm{56}\end{pmatrix}

 

Applications of the Hessian matrix

You may be wondering… what is the Hessian matrix for? Well, the Hessian matrix has several applications in mathematics. Next, we will see what the Hessian matrix is used for.

Minimum, maximum or saddle point

If the gradient of a function is zero at some point, that is f(x)=0, then function f has a critical point at x. In this regard, we can determine whether that critical point is a local minimum, a local maximum or a saddle point using the Hessian matrix:

  • If the Hessian matrix is positive definite (all the eigenvalues of the Hessian matrix are positive), the critical point is a local minimum of the function.
  • If the Hessian matrix is negative definite (all the eigenvalues of the Hessian matrix are negative), the critical point is a local maximum of the function.
  • If the Hessian matrix is indefinite (the Hessian matrix has positive and negative eigenvalues), the critical point is a saddle point.

Note that if an eigenvalue of the Hessian matrix is 0, we cannot know whether the critical point is a extremum or a saddle point.

Convexity or concavity

Another utility of the Hessian matrix is to know whether a function is concave or convex. And this can be determined applying the following theorem.

Let A\subseteq\mathbb{R}^n be an open set and f \colon A \to \mathbb{R} a function whose second derivatives are continuous, its concavity or convexity is defined by the Hessian matrix:

  • Function f is convex on set A if, and only if, its Hessian matrix is positive semidefinite at all points on the set.
  • Function f is strictly convex on set A if, and only if, its Hessian matrix is positive definite at all points on the set.
  • Function f is concave on set A if, and only if, its Hessian matrix is negative semi-definite at all points on the set.
  • Function f is strictly concave on set A if, and only if, its Hessian matrix is negative definite at all points on the set.

Taylor polynomial

The expansion of the Taylor polynomial for functions of 2 or more variables at the point a begins as follows:

\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots

As you can see, the second order terms of the Taylor expansion are given by the Hessian matrix evaluated at point a. This application of the Hessian matrix is very useful in large optimization problems.

Bordered Hessian matrix

Another use of the Hessian matrix is to calculate the minimum and maximum of a multivariate function f(x,y) restricted to another function g(x,y). To solve this problem, we use the bordered Hessian matrix, which is calculated applying the following steps:

Step 1: Calculate the Lagrange function, which is defined by the following expression:

\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)

Step 2: Find the critical points of the Lagrange function. To do this, we calculate the gradient of the Lagrange function, set the equations equal to 0, and solve the equations.

\displaystyle \nabla L = 0

\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0

Step 3: For each point found, calculate the bordered Hessian matrix, which is defined by the following formula:

\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}

Step 4: Determine for each critical point whether it is a maximum or a minimum:

  • The critical point will be a local maximum of function f under the restrictions of function g if the last n-m (where n is the number of variables and m the number of constraints) major minors of the bordered Hessian matrix evaluated at the critical point have alternating signs starting with the negative sign.
  • The critical point will be a local minimum of function f under the restrictions of function g if the last n-m (where n is the number of variables and m the number of constraints) major minors of the bordered Hessian matrix evaluated at the critical point all have negative signs.

Note that the local minimums or maximums of a restricted function do not have to be that of the unrestricted function. So the bordered Hessian matrix only works for this type of problems.

Leave a Comment

Your email address will not be published. Required fields are marked *