Leading coefficient of a polynomial

On this post we explain what the leading coefficient of a polynomial is and how to find it. Also, you will see several examples on how to identify the leading coefficient of a polynomial.

What is the leading coefficient of a polynomial?

The definition of leading coefficient of a polynomial is as follows:

In mathematics, the leading coefficient of a polynomial is the coefficient of the term with the highest degree of the polynomial, that is, the leading coefficient of a polynomial is the number that is in front of the x with the highest exponent.

For example, the leading coefficient of the following polynomial is 5:

The highest degree term of the above polynomial is 5x³ (monomial of degree 3), therefore the coefficient of the maximum degree term is 5. And, consequently, the leading coefficient of the polynomial is equal to 5.

Note that if a polynomial is in standard form, the leading coefficient will always be the coefficient of the first term.

Moreover, the term with the highest degree is also called leading term. Thus, the leading coefficient is the coefficient of the leading term of the polynomial.

As you can see, to determine the leading coefficient of a polynomial you must know how to calculate the degree of all the terms of a polynomial. When the polynomial has only one variable is quite easy, but finding the leading coefficient when the polynomial has two or more variables it is more complicated. You can see how to calculate the degree of a term with two variables in the following link:

➤ See: degree of a polynomial with two variables

Examples of how to find the leading coefficient of a polynomial

Once we know how to identify the leading coefficient of a polynomial, let’s practice with several solved examples.

• Example of the leading coefficient of a polynomial of degree 4:

The highest degree term of the polynomial is 3x ⁴, so the leading coefficient of the polynomial is 3.

• Example of the leading coefficient of a polynomial of degree 5:

The term with the maximum degree of the polynomial is 8x⁵, therefore, the leading coefficient of the polynomial is 8.

• Example of the leading coefficient of a polynomial of degree 7:

The highest degree element of the polynomial is -6x ⁷, thus, the leading coefficient of the polynomial is -6. Note that the negative sign is also part of the coefficient.

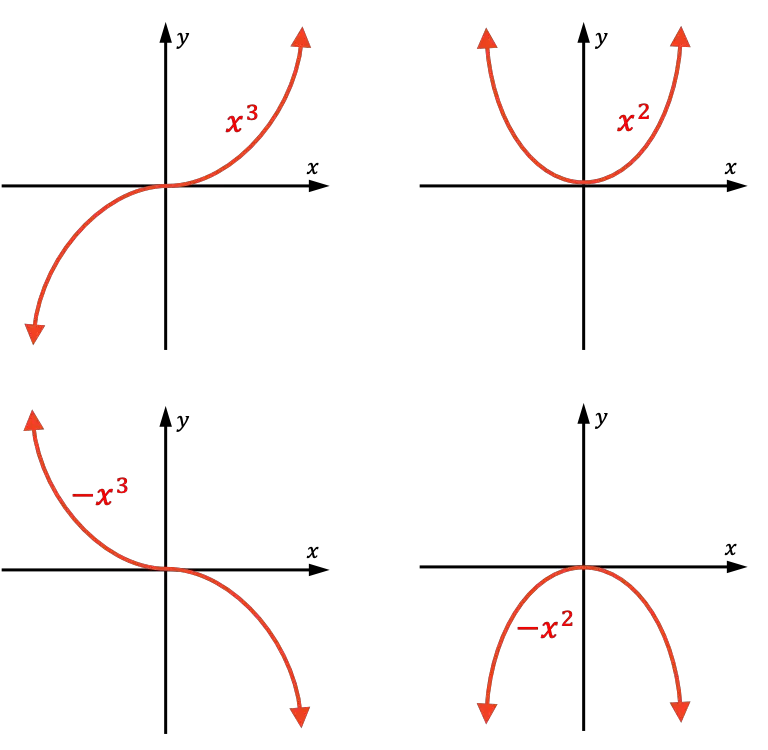
Leading coefficients and graphs

The graph of a polynomial function depends on the sign of the leading coefficient and the exponent of the leading term as follows:

• If the leading coefficient is positive and the exponent of the leading term is odd, the graph falls to the left and rises to the right.
• If the leading coefficient is negative and the exponent of the leading term is odd, the graph rises to the left and falls to the right.
• If the leading coefficient is positive and the exponent of the leading term is even, the graph rises to the left and right.
• If the leading coefficient is negative and the exponent of the leading term is even, the graph falls to the left and right.