▷ What are like terms? (definition and examples)

Here you will find the explanation of what like terms are. In addition, you will see examples of like terms and solved exercises of this type of monomials.

Table of Contents

What are like terms?

The definition of like terms is as follows:

Like terms are terms that have exactly the same variables and the same exponents.

For example, the terms 5x³ and 2x³ are the like terms because they have the same variable (x) and their exponents are also equivalent (3).

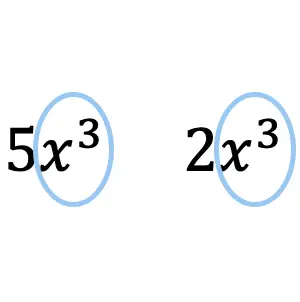
Note that it is not necessary for two like terms to have the same coefficient, as long as they have the same variables and exponents, they will be like terms.

Moreover, the order in which the variables appear does not matter, in other words, two terms that have the same variables (and the same exponents) but expressed in different order are also like terms. For example, the term 12x²y⁵ and the term -4y⁵x² are like terms.

$12\color{red}\bm{x^2}\color{blue}\bm{y^5} \qquad \color{black}-4\color{blue}\bm{y^5}\color{red}\bm{x^2}$

On the other hand, if two terms have different variables or powers, they are called unlike terms.

One of the characteristics of like terms is that they can be combined, that is, we can add or subtract like terms. To do this, we simply have to add their coefficients, and their variables and powers remain the same.

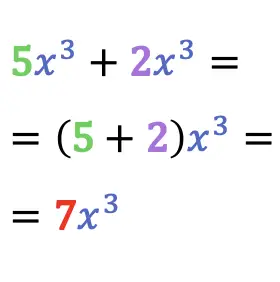
Examples of like terms

To fully understand the meaning in math of like terms, below you can see several examples of how to combine like terms:

Example 1

$4x^5\qquad -2x^5$

The 2 terms above are like terms and, therefore, we can combine them.

$4x^5-2x^5=2x^5$

Example 2

$7xy^3\qquad 8xy^3\qquad -6xy^3$

The above three terms are like terms, since they are composed of the same variables and exponents, so we can simplify them to a single term.

$7xy^3+8xy^3-6xy^3=15xy^3-6xy^3=9xy^3$

Example 3

$12a^6b^2c^7 \qquad -4a^6c^7b^2$

$-5c^7a^6b^2 \qquad 3b^2a^6c^7$

The variables of the terms are expressed in different order, but they are alike. So we can express the variables of the

$12a^6b^2c^7 \qquad -4a^6b^2c^7$

$-5a^6b^2c^7 \qquad 3a^6b^2c^7$

These four terms are like terms because they have the same variables raised to the same exponents, thus, we can combine them by adding or subtracting their coefficients:

$12a^6b^2c^7-4a^6b^2c^7-5a^6b^2c^7+3a^6b^2c^7=6a^6b^2c^7$

Practice problems of like terms

Problem 1

Match the pairs of terms that are like terms:

$\begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}$