▷ How to multiply monomials (examples and practice problems)

Here we explain how to multiply monomials. Also, you will see several examples of multiplication of monomials and exercises solved step by step. Finally, you will find the properties of the product of monomials.

Table of Contents

How to multiply monomials

The multiplication of monomials is done as follows:

In mathematics, the multiplication of two monomials results in another monomial whose coefficient is the product of the coefficients of the monomials and whose variable is obtained by multiplying the variables that have the same base, that is, by adding their exponents.

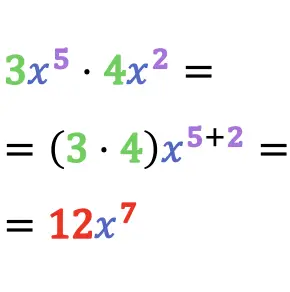
Therefore, to multiply two monomials with the same base, simply multiply the coefficients of the monomials and add the exponents of their powers.

However, if we multiply two monomials with different base, we have to multiply their coefficients and leave the powers equal. For example:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Logically, in the product of the coefficients of the monomials the sign rules also apply, since multiplication consists of an arithmetic operation. Thus:

A positive monomial times another positive monomial is equal to a positive monomial:

$2x^6\cdot 4x^3 = 8x^9$

A positive monomial times a negative monomial (or vice versa) is equivalent to a negative monomial:

$-2x^6\cdot 4x^3 = -8x^9$

$2x^6\cdot (-4x^3) = -8x^9$

Two negative monomials multiplied result in a positive monomial:

$-2x^6\cdot (-4x^3) = 8x^9$

Examples of multiplication of monomials

So that you can fully understand how to do a multiplication of monomials, below we leave you with several examples of this type of operation:

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Practice problems on multiplication of monomials

Below you have several practice problems solved step by step of multiplication of monomials:

Problem 1

Calculate the following multiplications of monomials:

$\text{A)} \ 3x^4\cdot x^5$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ 5x^7\cdot 6x^2$

$\text{D)} \ -4a^3 \cdot (-2a)$

See solution

$\text{A)} \ 3x^4\cdot x^5 = (3\cdot 1)x^{4+5} = \bm{3x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{D)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

Problem 2

Multiply the following monomials:

$\text{A)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{B)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{C)} \ 3b^2 \cdot (-3b^2) \cdot 6 b^4$

$\text{D)} \ 7x^3 \cdot 3x^2 \cdot 2x^7$

See solution

$\text{A)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{B)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{C)} \ 3b^2 \cdot (-3b^2) \cdot 6 b^4=-9b^4\cdot 6 b^4 =\bm{ -54b^8}$

$\text{D)} \ 7x^3 \cdot 3x^2 \cdot 2x^7 = 21x^5\cdot 2x^7 = \bm{42x^{12}}$

Problem 3

Simplify the following multiplications of monomials as much as possible:

$\text{A)} \ 8x^3y^2 \cdot 5x^4y^7$

$\text{B)} \ -6x^5y^2z \cdot (-4x^4y^9z^2)$

$\text{C)} \ -4a^3b^8 \cdot 5 a^3c^2$

$\text{D)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

See solution

$\text{A)} \ 8x^3y^2 \cdot 5x^4y^7 = \bm{40x^7y^9}$

$\text{B)} \ -6x^5y^2z \cdot (-4x^4y^9z^2) = \bm{24x^9y^{11}z^3}$

$\text{C)} \ -4a^3b^8 \cdot 5 a^3c^2 = \bm{-20a^6b^8c^2}$

$\text{D)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)=$ $35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =$ $\bm{-70x^{13}y^7z^7}$

Properties of multiplication of monomials

The product of monomials has the following properties:

Commutative property: the order of the multiplication of the monomials does not alter the result of the multiplication.

$3x^5 \cdot 2x^4 = 6x^9$

$2x^4 \cdot 3x^5 = 6x^9$

Associative Property: when three or more monomials are multiplied, the result is the same regardless of how the factors are multiplied:

$(2x \cdot 4x^2) \cdot 3x^5 = 24x^8$

$2x \cdot (4x^2 \cdot 3x^5) = 24x^8$

Distributive property: the sum of two monomials multiplied by a third is equal to the sum of each addend multiplied by the third monomial.

$4x^6 \cdot (3x^4+5x^4) = 4x^6 \cdot 3x^4 + 4x^6 \cdot 5x^4$

Multiplying monomials

How to multiply monomials

Examples of multiplication of monomials

Practice problems on multiplication of monomials

Problem 1

Problem 2

Problem 3

Properties of multiplication of monomials

Leave a Comment Cancel Reply