▷ Powers of Monomials (practice)

Here we explain how to find the power of a monomial. Also, you will see several examples of powers of monomials and exercises with solutions to practice.

Table of Contents

How to calculate the power of a monomial

To calculate the power of a monomial, raise each element of the monomial to the exponent of the power. That is, the power of a monomial consists of raising the coefficient and the variable of the monomial to the exponent of the power.

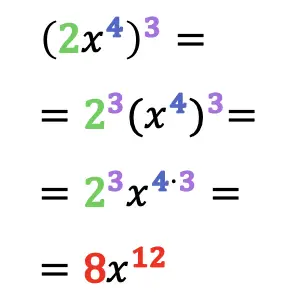
Remember from the properties of powers that when we raise a term that is already raised, the two exponents multiply each other. That is why in the powers of monomials the exponent of each variable (letter) is always multiplied by the exponent that indicates the power.

Note that the result of the power of a monomial depends on the sign of the monomial:

The power of a positive monomial always results in another positive monomial, regardless of the parity of the exponent:

$\left(3x^5\right)^2 = 3^2\left(x^5\right)^2 = 9x^{10}$

$\left(3x^5\right)^3 = 3^3\left(x^5\right)^3 = 27x^{15}$

A negative monomial raised to an even power equals to a positive monomial:

$\left(-3x^5\right)^2 = (-3)^2\left(x^5\right)^2 = 9x^{10}$

A negative monomial raised to an odd power is always equal to another negative monomial:

$\left(-3x^5\right)^3 = (-3)^3\left(x^5\right)^3 = -27x^{15}$

Examples of powers of monomials

So that you can fully understand how to compute the power of a monomial, below we leave you with several examples of this type of operation with monomials:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Practice problems on powers of monomials

Below you have several practice problems on finding powers of monomials to understand better how to do this operation.

Problem 1

Calculate the following powers of monomials

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(2x^5\right)^4$

$\text{C)} \ \left(-2a^7\right)^3$

$\text{D)} \ \left(7x^3\right)^3$

Ver solución

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(2x^5\right)^4=2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = \bm{16x^{20}}$

$\text{C)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{D)} \ \left(7x^3\right)^3 =7^3\left(x^3\right)^3 = 7^3x^{3\cdot 3} = \bm{343x^{9}}$

Problem 2

Solve the following powers of monomials

$\text{A)} \ \left(5x^8y^2\right)^3$

$\text{B)} \ \left(-x^3y^5z^4\right)^6$

$\text{C)} \ \left(-3x^3yz\right)^3$

$\text{D)} \ \left(-2x^5y^4\right)^5$

Ver solución

$\text{A)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{B)} \ \left(-x^3y^5z^4\right)^6=(-1)^6\left(x^3y^5z^4\right)^6 = \bm{x^{18}y^{30}z^{24}}$

$\text{C)} \ \left(-3x^3yz\right)^3=(-3)^3\left(x^3yz\right)^3 = \bm{-27x^9y^3z^3}$

$\text{D)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Problem 3

Simplify the following powers of fractions with monomials as much as possible:

$\displaystyle\text{A)} \ \left(\frac{x^2}{y}\right)^4$

$\displaystyle\text{B)} \ \left(\frac{3x^5}{6y^3}\right)^2$

$\displaystyle\text{C)} \ \left(\frac{4x^3y^6}{-x^2z^5}\right)^2$

See: how to divide monomials

Ver solución

To simplify the rational expressions we have to apply the following property of powers:

$\displaystyle\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$

Thus:

$\displaystyle\text{A)} \ \left(\frac{x^2}{y}\right)^4=\frac{\left( x^2\right)^4}{y^4}=\frac{\bm{x^8}}{\bm{y^4}}$

$\displaystyle\text{B)} \ \left(\frac{3x^5}{6y^3}\right)^2 =\frac{\left(3x^5\right)^2}{\left(6y^3\right)^2}=\frac{9x^{10}}{36y^6}=\frac{\bm{x^{10}}}{\bm{4y^6}}$

$\displaystyle\text{C)} \ \left(\frac{4x^3y^6}{-x^2z^5}\right)^2 =\frac{\left(4x^3y^6\right)^2}{\left(-x^2z^5\right)^2}= \frac{16x^6y^{12}}{x^4z^{10}}=\frac{\bm{16x^2y^{12}}}{\bm{z^{10}}}$

Powers of monomials

How to calculate the power of a monomial

Examples of powers of monomials

Practice problems on powers of monomials

Problem 1

Problem 2

Problem 3

Leave a Comment Cancel Reply