On this post we explain what antisymmetric matrices are. In addition, you will see several examples along with its typical form to understand it perfectly. We also explain what is special about the calculation of the determinant of an antisymmetric matrix and all the properties of this type of matrix. And finally, you will find how to decompose any square matrix into the sum of a symmetric matrix plus another antisymmetric matrix.
Table of Contents
What is an antisymmetric matrix?
The definition of antisymmetric matrix is as follows:
An antisymmetric matrix is a square matrix whose transpose is equal to its negative.
Where represents the transpose matrix of
and
is matrix
with all its elements changed sign.
See: definition of transpose of a matrix.
In mathematics, antisymmetric matrices are also called skew-symmetric or antimetric matrices.
Examples of antisymmetric matrices
Once we know the meaning of antisymmetric matrix, let’s see several examples of antisymmetric matrices to fully understand the concept:
Example of an antisymmetric matrix of order 2
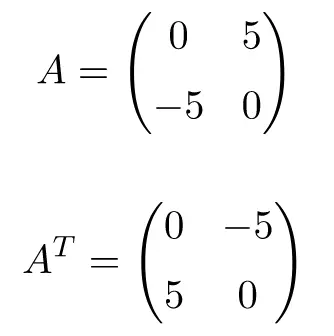
Example of 3×3 dimension antisymmetric matrix
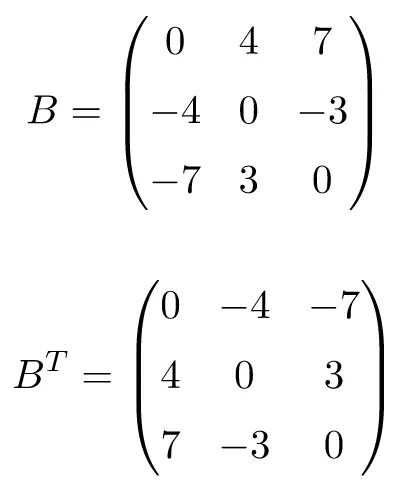
Example of 4×4 size antisymmetric matrix
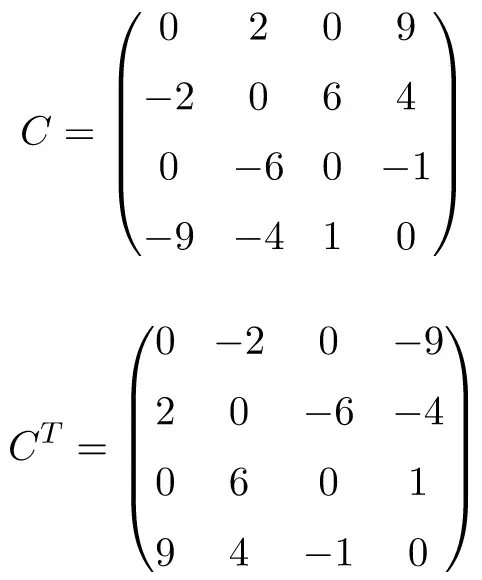
Transposing matrices A, B and C show that they are antisymmetric (or skew symmetric), because the transposed matrices are equivalent to their respective original matrices with the sign changed.
Form of an antisymmetric matrix
For the antisymmetric matrix condition to be fulfilled, they must always have the same type of form: the numbers on the main diagonal are all equal to zero and the element in row i and column j is the negative of the element in row j and column i. That is, the shape of the antisymmetric matrices is as follows:
Therefore, the main diagonal of an antisymmetric matrix acts as axis of antisymmetry. And this is where the name of this peculiar matrix comes from.
Determinant of an antisymmetric matrix
The determinant of an antisymmetric matrix depends on the dimension of the matrix. This is due to the properties of the determinants:
So if the antisymmetric matrix is of odd order, its determinant will be equal to 0. But if the antisymmetric matrix is of even dimension, the determinant can take any value.
Therefore, an odd-dimensional antisymmetric matrix is a non-invertible matrix. In contrast, an antisymmetric matrix of even order is always an invertible matrix.
Properties of antisymmetric matrices
The characteristics of the antisymmetric matrices are as follows:
- The addition (or subtraction) of two antisymmetric matrices results in another antisymmetric matrix, since transposing two added (or subtracted) matrices is equivalent to transposing each matrix separately:
- Any antisymmetric matrix multiplied by a scalar also results in another antisymmetric matrix.
- The power of an antisymmetric matrix is equivalent to an antisymmetric matrix or a symmetric matrix. If the exponent is an even number the result of the power is a symmetric matrix, but if the exponent is an odd number the result of the potentiation is an antisymmetric matrix.
See: what is a symmetric matrix?
- The trace of an antisymmetric matrix is always equal to zero.
- The sum of any antisymmetric matrix plus the unit matrix results in an invertible matrix.
- All real eigenvalues of an antisymmetric matrix are 0. However, an antisymmetric matrix can also have complex eigenvalues.
See: properties of eigenvalues.
- All antisymmetric matrices are normal matrices. Therefore, they are subject to the spectral theorem, which states that an antisymmetric matrix is diagonalizable by the identity matrix.
See: how to diagonalize a matrix.
Decomposition of a square matrix into a symmetric and an antisymmetric matrix
A peculiarity that square matrices have is that they can be decomposed into the sum of a symmetric matrix plus an antisymmetric matrix.
The formula that allows us to do it is the following:
Where C is the square matrix that we want to decompose, CT its transpose, and finally S and A are the symmetric and antisymmetric matrices respectively into which matrix C is decomposed.
Below you have a solved exercise to prove the above formula. We are going to decompose the following matrix:
We calculate the symmetric and antisymmetric matrices with the formulas:
And we can check that the equation is satisfied by adding both matrices:
✅