▷ Identity (or Unit) matrix: definition, properties, operations, applications,...

On this post you will see what the identity (or unit) matrix is with several examples. In addition, we explain all the properties of the identity matrix, how to operate with this type of matrix and how to find its determinant. Finally, you will see the applications that this special matrix has.

Table of Contents

What is the Identity matrix?

The definition of identity matrix (or unit matrix) is as follows:

The identity matrix, also called unit matrix, is a square matrix in which all elements are zeros (0) except on the main diagonal, where all elements are ones (1).

Examples of identities matrices

Once we know the meaning of identity matrix, let’s see some examples of this type of matrix:

2×2 identity matrix

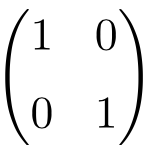
3×3 identity matrix

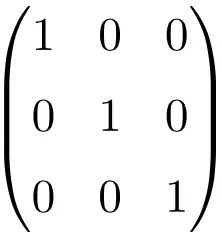
4×4 identity matrix

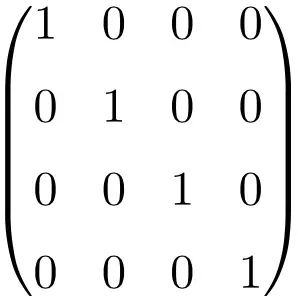
As you can see, to find the Identity matrix you always have to do the same procedure: put ones (1) on the main diagonal and the rest all zeros (0). The only thing that changes is the dimension of the identity matrix.

Properties of the identity matrix

The identity matrix, also known as unit matrix, is widely used in mathematics, and that is due to the characteristics that this type of matrix has:

The identity matrix is an example of a diagonal matrix.

The identity matrix is an upper and lower triangular matrix at the same time.

The identity matrix is also a symmetric matrix.

The identity matrix has full rank, that is, the rank of the identity matrix equals to its order. For example, the identity matrix of order 2 has rank of 2, and the identity matrix of order 3 has rank of 3.

The adjugate matrix of the Identity matrix is itself.

$\displaystyle \text{Adj}(I) =I$

The identity matrix is an invertible matrix. And the inverse of the identity matrix is itself:

$\displaystyle I^{-1}=I$

See: meaning of invertible matrix

Any scalar matrix can be obtained from the multiplication of a number by the identity matrix:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

All eigenvalues of the identity matrix are 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Finally, the identity matrix is also an example of a permutation matrix.

Operations with the identity matrix

Surely you are thinking: this is all very good but … what is the point of the identity matrix? If it’s only a matrix with zeros and ones!

The identity matrix is used a lot in mathematics, in fact, this type of square matrix is very important in linear algebra. The main utility of the Identity matrix is the ease with which it allows you to perform matrix operations calculations. Let’s see how to operate with the identity matrix:

Addition and subtraction with the Identity matrix

One way to add (or subtract) numbers on the main diagonal of a matrix without modifying the other elements is through the identity matrix, since it only adds (or subtracts) one unit to those elements:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

You can also add or subtract more units to the elements on the main diagonal by first multiplying the identity matrix by a scalar:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Multiplication of a matrix by the Identity matrix

When multiplying any matrix by the Identity matrix, it acts as a neutral element, that is, any matrix multiplied by the identity matrix results in the same matrix. Take a look at the following example:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

In addition, the order of the matrix product is indifferent, in other words, it does not matter if we multiply the identity matrix from the right or from the left, the result will always be the same matrix. To prove this, we repeat the previous exercise but this time multiplying the identity matrix from the opposite side:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Power of the identity matrix

The power of the identity matrix always results in the identity matrix, regardless of the dimension of the identity matrix and the exponent to which the matrix is raised. Thus, the identity matrix is idempotent.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Determinant of the Identity matrix

The determinant of the identity (or unit) matrix is always equal to 1, regardless of the dimension of the identity matrix.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$}\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Applications of the Identity matrix

As you may have observed, the identity matrix has many uses and that is why it is so interesting. One of the benefits of the unit matrix is the operations, since, as we have seen above, it is very easy to perform matrix operations with it.

Moreover, the identity matrix is also used to calculate the inverse matrix with the Gaussian elimination method. This method is based on placing a matrix next to the identity array, thus forming a larger array. Then you have to transform the original matrix into the identity matrix by applying elementary operations on the rows.

Finally, the identity matrix is also useful for diagonalizing a matrix and calculating its eigenvalues. Because through operations, in which the identity matrix takes part, the characteristic polynomial can be calculated (from which the eigenvalues are obtained). But this is already a very advanced theme, that’s why we have a whole super extensive page dedicated to the diagonalization of matrices with examples and solved exercises explaining it.

Identity (or unit) matrix