▷ What is the complex conjugate transpose of a matrix? ✅

In this post we explain what a conjugate transpose matrix is and how to calculate the complex conjugate transpose of a matrix. Also, we show you an example of the conjugate transpose of a matrix and all the properties of this type of matrix.

Table of Contents

What is a conjugate transpose matrix?

In mathematics, the conjugate transpose of a matrix is calculated by taking the transpose of the matrix and then taking the complex conjugate of all of its entries.

The complex conjugate transpose matrix is also called Hermitian transpose. In addition, this type of matrix is usually denoted by A^H or A*.

On the other hand, the complex conjugate transpose matrix is different from the conjugate matrix.

Example of the conjugate transpose of a matrix

Here is an example of how to find the conjugate transpose of a matrix:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

First, we transpose matrix A:

$\displaystyle A^T=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

And then we calculate the complex conjugate of the transpose, that is, we change the sign of the imaginary part of all complex numbers:

$\displaystyle A^H=\overline{A^T}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

Thus, the summary of the calculation of the conjugate transpose matrix is:

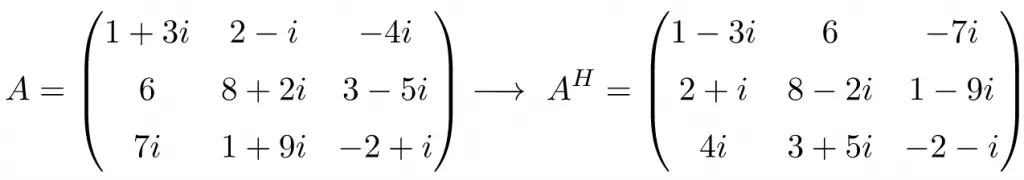
example of a 3x3 complex conjugate transpose matrix

Properties of the conjugate transpose matrix

The characteristics of the conjugate transpose matrix are as follows:

The conjugate transpose of a previously transposed and conjugated matrix equals to the original matrix.

$\displaystyle \bigl(A^H\bigr)^H = A$

The addition property of conjugate transpose matrices states that doing the addition (or subtraction) of two matrices and then conjugate and transpose the result is the same as first doing the conjugate transpose of each matrix and then adding (or subtracting) the results.

$\displaystyle \bigl( A\pm B \bigr)^H = A^H\pm B^H$

See: matrix addition and subtraction

Multiplying two matrices and then doing their conjugate transpose gives the same result as the inverse product of the conjugate transpose matrices.

$\displaystyle \bigl( A\cdot B \bigr)^H = B^H\cdot A^H$

See: properties of matrix multiplication

Calculating the conjugate transpose of the product of a scalar by a matrix is identical to conjugating the complex number and finding the conjugate transpose of the matrix separately and then doing the multiplication.

$\displaystyle \bigl( k\cdot A \bigr)^H = \overline{k}\cdot A^H$