On this post you will find the explanation of what a nilpotent matrix is, as well as several examples so that you can completely understand it. In addition, you will see the formula that nilpotent matrices have and all the properties that these types of matrices have.
Table of Contents
What is a nilpotent matrix?
The definition of a nilpotent matrix is as follows:
A nilpotent matrix is a square matrix that raised to some integer results in the null matrix.
Where is the nilpotent matrix and
the exponent of the power that results in the null matrix.
See definition of null matrix.
This condition does not mean that the power of a nilpotent matrix always gives zero regardless of the exponent, but that if there is at least one power of the matrix whose result is a matrix filled with 0s then the matrix is nilpotent.
On the other hand, the nilpotenciy index of a nilpotent matrix is the smallest number with which the nilpotency condition is fulfilled. It can also be said that the nilpotent matrix is of index k (where k is its nilpotency index).
Examples of nilpotent matrices
To understand the concept of a nilpotent matrix, we are going to see several examples of this type of matrix:
Example of a 2×2 nilpotent matrix
The following square matrix of order 2 is nilpotent:
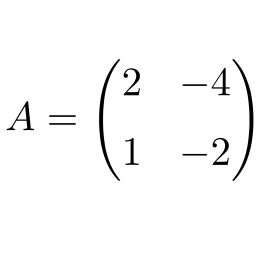
The matrix is nilpotent because by squaring matrix A we get the zero matrix as a result:
Therefore, it is a nilpotent matrix and its nilpotency index is 2, since the null matrix is obtained with the second power.
Example of a 3×3 nilpotent matrix
The following square matrix of order 3 is nilpotent:
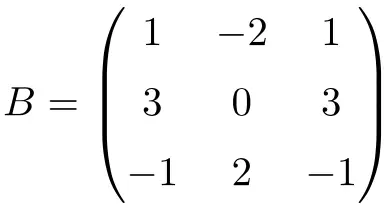
Although when raising the matrix to 2 we do not obtain the null matrix:
When calculating the cube of the matrix we do get a matrix with all the elements equal to 0:
So matrix B is a nilpotent matrix, and since the null matrix is obtained with the third power, its nilpotency index is 3.
Formula of a 2×2 nilpotent matrix
Below you can see the form that all nilpotent matrices have. Its proof is a bit tedious, so we give you directly the formula to find a nilpotent matrix of order 2:
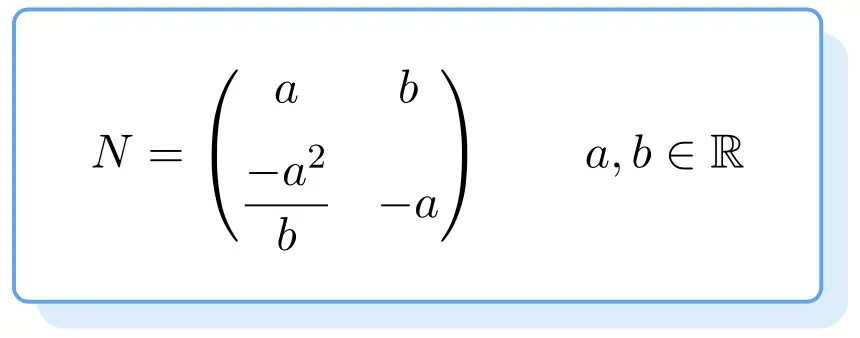
So any matrix that checks the above formula will be a nilpotent matrix. To do this, the values and
can be any as long as they are real numbers.
Properties of nilpotent matrices
All nilpotent matrices have the following characteristics:
- The trace of a nilpotent matrix is always zero.
- Similarly, the determinant of any nilpotent matrix is always equal to 0. However, the reciprocal is not true, that is, that the determinant of a matrix is zero does not imply that the matrix is nilpotent.
- The only diagonalizable nilpotent matrix is the null matrix.
- The nilpotency index of a nilpotent matrix of dimension n×n is always equal to or less than n. So the nilpotency index of a 2×2 nilpotent matrix will always be 2.
- A nilpotent matrix is not invertible.
- Any triangular matrix with zeros on the main diagonal is also a nilpotent matrix at the same time.
See definition of triangular matrix.
- There is a theorem that states that if the matrix
is nilpotent, then the matrix
is invertible, where
is the Identity matrix. Furthermore, its inverse matrix can be found with the following formula:
- Equivalently, if
is a nilpotent matrix, then the inverse of the
matrix can be calculated with the following equation:
- Every singular matrix can be decomposed into the product of nilpotent matrices.
- All eigenvalues of a nilpotent matrix are zero.
- Finally, as a curiosity, there is also the concept of nilpotent transformation, which defines a linear map
of a vector space such that
.
See also: