▷ What is an Idempotent matrix? ✅ (examples and properties)

On this post we explain what idempotent matrices are. We also show you several examples of this type of matrix so that you understand it perfectly. Furthermore you will find the formula to calculate an idempotent matrix and, finally, all the properties of idempotent matrices.

Table of Contents

What is an idempotent matrix?

The definition of idempotent matrix is as follows:

An idempotent matrix is a matrix that multiplied by itself results in the same matrix.

$A \cdot A = A$ .

Therefore, any power of an idempotent matrix is equal to the matrix itself, regardless of the exponent:

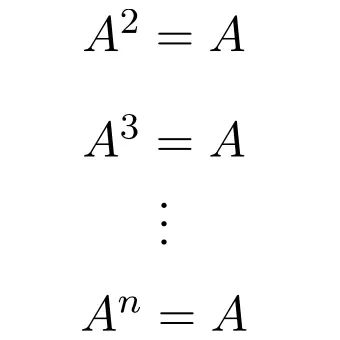
See how to calculate the power of a matrix.

In fact, this type of matrix receives this name because in mathematics idempotence is a property of certain operations that means that the same result is always obtained regardless of the number of times it is performed.

Examples of idempotent matrices

Once we know the concept of the idempotent matrix, we are going to see some examples of different dimensions:

Example of 2×2 idempotent matrix

The following square matrix of dimension 2×2 is idempotent:

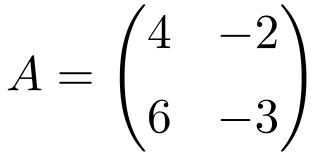
To check whether it is an idempotent matrix, we calculate its square:

$\displaystyle A^2 = \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & -3 \end{pmatrix}$

The result is identical, so it is shown that the matrix is idempotent.

Example of 3×3 idempotent matrix

The following square matrix of order 3 is idempotent:

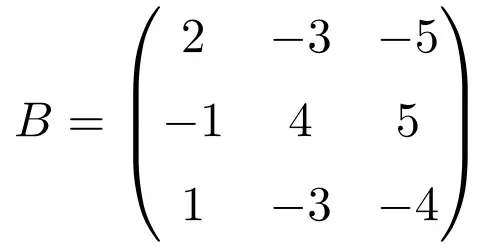
example of an idempotent matrix of dimension 3x3

To verify that it really is an idempotent matrix, we raise the matrix to 2:

$\displaystyle B ^ 2 = \begin{pmatrix} 2 & -3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

The result is the same as the original matrix, so the idempotency of the matrix is proven.

Formula for a 2×2 idempotent matrix

Here is the formula to obtain an idempotent matrix. The proof of the formula is a bit tedious, so we give you directly the formula to find an idempotent matrix:

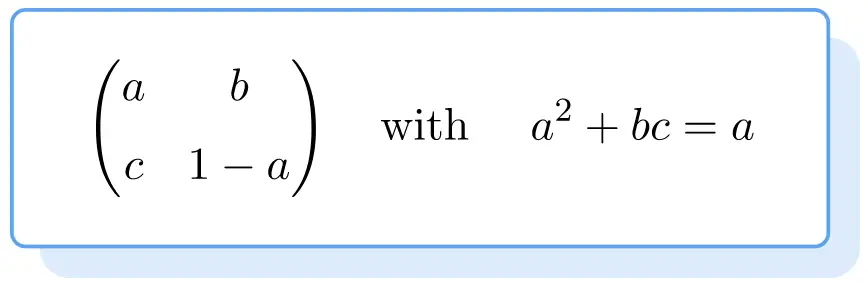
So the elements of the secondary diagonal of an idempotent matrix can be any as long as the condition $a ^ 2 + bc = a$ is met, and the numbers of the main diagonal must be $a$ y $1-a.$

In addition to all the matrices described by this formula, we must add the identity matrix of order 2, which is also an idempotent matrix despite not meeting the formula.

Properties of idempotent matrices

Idempotent matrices have the following characteristics:

The determinant of an idempotent matrix is always equal to 0 or 1.
Except for the Identity matrix, all other idempotent matrices are singular or degenerate matrices.
Any idempotent matrix is a diagonalizable matrix, and its eigenvalues are always 0 or 1.
The trace of an idempotent matrix is equal to the rank of the matrix.
Finally, there is a relationship between idempotent matrices and involutory matrices: the matrix $A$ is idempotent if, and only if, the matrix $\displaystyle P = 2A-I$ is involutory.

Idempotent matrix