Parts of an algebraic expression

Here we explain all the parts of an algebraic expression. Also, you will find several practice problems on identifying the parts of an algebraic expression.

Before seeing what are the parts of an algebraic expression, remember that an algebraic expression is a combination of numbers, variables and algebraic operations (addition, subtraction, multiplication, division and exponentiation).

What are the parts of an expression?

The parts of an algebraic expression are as follows:

• Variables: the variables of an algebraic expression are letters that represent numbers.
• Coefficients: the coefficients of an algebraic expression are the numbers that multiply the variables.
• Constant: a constant of an algebraic expression is a number that is not multiplied by any variable.
• Term: a term can be a variable, a constant or the product of a number and a variable (or variables).
• Degree: the degree of an algebraic expression is the highest degree of its terms.

Note: the degree of a term depends on the number of variables it has. If the term has only one variable, its degree is the exponent of that variable. On the other hand, if the term has two or more variables, its degree is the sum of the exponents of its variables. Finally, if the term has no variable, its degree is zero.

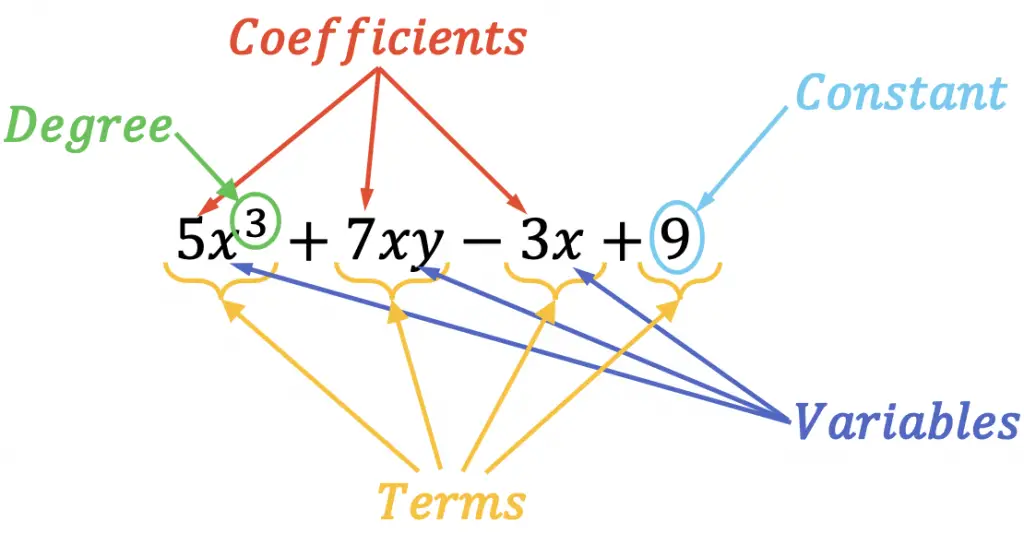
The previous algebraic expression has four terms: 5x³, 7xy, -3x and 9. Therefore, the variables of the expression are x and y, and its coefficients are 5, 7 and -3. Also, the expression has one constant, the number 9. And finally, the degree of the expression is 3 because the term with the highest degree is 5x³, whose degree is three.

When two terms have the same variables with the same exponents are called like terms.

➤ Examples of like terms

Moreover, when an expression has a multiplication, each term that is multiplied is called factor. For example, the multiplication has three factors: the constant 9, the parenthesis and the term

Practice problems on identifying parts of an expression

To understand better the concept of parts of an expression, we are going to see several examples of how to identify the parts of an algebraic expression:

Problem 1

Identify the parts of the following algebraic expression:

• Variable: x
• Coefficients: 4, -8
• Constant: 4
• Terms: 4x², -8x, 1
• Degree: 2

Problem 2

Name the parts of the following algebraic expression:

• Variables: a, b, c
• Coefficients: 4, -5, 1, 6
• Constant: -7
• Terms: 4b⁴, -5ab, c, 6abc, -7
• Degree: 4

As you can see in this exercise, when a term does not have a number in front of it, it means that its coefficient is the number 1. For example, the coefficient of the term is 1.

Problem 3

Identify all the parts of the following algebraic expression:

• Variables: x, y, x
• Coefficients: 3, 2, -5, 10
• Constant: 1
• Terms: 3xyz, 2x³y, -5x⁶y³, 10z⁷
• Degree: 9

The degree of the term 10z⁷ is 7, however, the degree of the term -5x⁶y³ is 9, since to find the degree of a term we have to add all the exponents of its variables. Thus, the degree of the expression is 9.