▷ How to compute determinants using the Rule of Sarrus

Here we explain what the Rule of Sarrus is and how to find the determinant of a 3×3 matrix using the Rule of Sarrus. In addition, we will discuss whether the Rule of Sarrus can also be used to compute a 4×4 determinant or not. And, finally, you will see solved exercises of 3×3 determinants applying this method.

Table of Contents

What is the Rule of Sarrus?

The Rule of Sarrus is a mnemonic rule for solving the determinant of a 3×3 matrix.

The Rule of Sarrus is also known as scheme of Sarrus or method of Sarrus, and it is named after Pierre Frédéric Sarrus, an important French mathematician of the XIX century.

How to find the determinant of a 3×3 matrix with the Rule of Sarrus

To find the determinant of a 3×3 matrix using the Rule of Sarrus, duplicate the first two columns of the matrix to the right of its third column. Then, add the products of the main diagonals going from top to bottom and subtract the products of the main diagonals going from bottom to top.

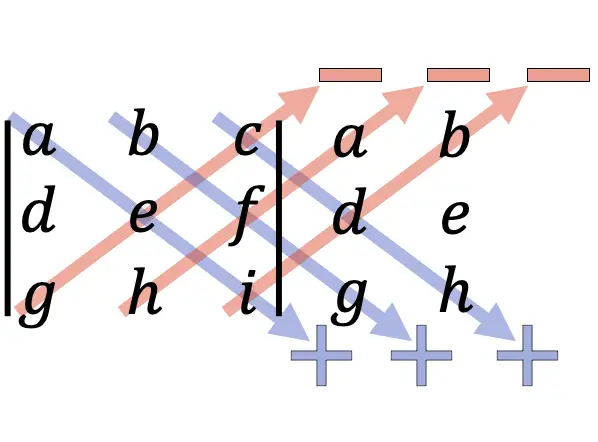
You can see how to apply the Rule of Sarrus with the following example:

$\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

First we rewrite the first two columns to the right of the 3×3 matrix:

$\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \ \begin{matrix}2 & 1\\[1.1ex] -1 & 1\\[1.1ex] -2 & 4\end{matrix}$

And then we add the products of the main diagonals going from top to bottom and subtract the products of the main diagonals going from bottom to top:

$\begin{aligned}\begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \ \begin{matrix}2 & 1\\[1.1ex] -1 & 1\\[1.1ex] -2 & 4 \end{matrix} \ & = \begin{array}{l}\\[2ex]2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + 3\cdot (-1) \cdot 4 \\[2ex] - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- 1\cdot (-1) \cdot 1\end{array} \\[2ex] & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & =-3 \end{aligned}$

However, this is not the only method out there to compute the determinant of a 3×3 matrix. See how to find the determinant of a 3×3 matrix using cofactor expansion.

Can the determinant of a 4×4 matrix be calculated with the Rule of Sarrus?

Typically 4×4 determinants take a lot of calculations and therefore a lot of time. So it would be very convenient if the Sarrus scheme could also be used to evaluate the determinant of a 4×4 matrix, since the Sarrus Rule is very easy to perform.

Unfortunately, the Rule of Sarrus cannot be used to directly compute the determinant of a 4×4 matrix. However, 4×4 determinants can be simplified into 3×3 determinants, to which we can apply the Sarrus’ Rule. To see how, check this example of a determinant of a 4×4 matrix.

Rule of Sarrus practice problems

Problem 1

Find the determinant of the following 3×3 matrix using the rule of Sarrus:

$\begin{vmatrix}5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0\end{vmatrix}$

See solution

First of all, we duplicate the first two columns of the matrix to its right:

$\begin{vmatrix} 5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0\end{vmatrix} \ \begin{matrix}5&0\\[1.1ex]1&3\\[1.1ex]-1&1\end{matrix}$

And then we apply the Sarrus’ rule:

$\begin{aligned}\begin{vmatrix} 5&0&2\\[1.1ex]1&3&4\\[1.1ex]-1&1&0 \end{vmatrix} \ \begin{matrix}5&0\\[1.1ex]1&3\\[1.1ex]-1&1\end{matrix} \ & = \begin{array}{l}\\[2ex]5 \cdot 3 \cdot 0 + 0 \cdot 4 \cdot (-1) + 2 \cdot 1 \cdot 1 \\[2ex] - (-1) \cdot 3 \cdot 2 - 1 \cdot 4 \cdot 5- 0 \cdot 1 \cdot 0 \end{array} \\[2ex] & =0+0+2+6-20+0\\[2ex] & =\bm{-12} \end{aligned}$

Problem 2

Compute the determinant of the following matrix of order 3 applying the rule of Sarrus:

$\begin{vmatrix}1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix}$

See solution

First we have to rewrite the first two columns of the matrix to its right:

$\begin{vmatrix} 1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix} \ \begin{matrix}1&3\\[1.1ex]5&1\\[1.1ex]2&-3\end{matrix}$

And then we perform the products of the Sarrus’ formula:

$\begin{aligned}\begin{vmatrix}1&3&-2\\[1.1ex]5&1&4\\[1.1ex]2&-3&2\end{vmatrix} \ \begin{matrix}1&3\\[1.1ex]5&1\\[1.1ex]2&-3\end{matrix} \ & = \begin{array}{l}\\[2ex]1 \cdot 1 \cdot 2 + 3 \cdot 4 \cdot 2 + (-2) \cdot 5 \cdot (-3) \\[2ex] - 2 \cdot 1 \cdot (-2) - (-3) \cdot 4 \cdot 1- 2 \cdot 5\cdot 3 \end{array} \\[2ex] & =2+24+30+4+12-30\\[2ex] & =\bm{42} \end{aligned}$

Problem 3

Evaluate the determinant of the following 3×3 square matrix with the rule of Sarrus:

$\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix}$

See solution

First we duplicate the first two columns of the matrix to its right:

$\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix} \ \begin{matrix}4&1\\[1.1ex]-2&6\\[1.1ex]3&2\end{matrix}$

And finally we use the Sarrus’ scheme to solve the 3×3 determinant:

$\begin{aligned}\begin{vmatrix}4&1&5\\[1.1ex]-2&6&1\\[1.1ex]3&2&-4\end{vmatrix} \ \begin{matrix}4&1\\[1.1ex]-2&6\\[1.1ex]3&2\end{matrix} \ & = \begin{array}{l}\\[2ex]4\cdot 6 \cdot (-4) + 1 \cdot 1 \cdot 3 + 5 \cdot (-2) \cdot 2 \\[2ex] - 3 \cdot 6 \cdot 5 - 2 \cdot 1 \cdot 4- (-4) \cdot (-2)\cdot 1 \end{array} \\[2ex] & =-96+3-20-90-8-8=\\[2ex] & =\bm{-219} \end{aligned}$

Do you know what Cramer’s rule is? It is a method to solve systems of linear equations based on computing 3×3 determinants. See how to use Cramer’s rule.

What is the Rule of Sarrus?

How to find the determinant of a 3×3 matrix with the Rule of Sarrus

Can the determinant of a 4×4 matrix be calculated with the Rule of Sarrus?

Rule of Sarrus practice problems

Problem 1

Problem 2

Problem 3

Leave a Comment Cancel Reply