▷ Involutory matrix: definition, examples, formula and properties

On this post we explain what an involutory matrix is. We also show you examples of 2×2, 3×3 and 4×4 involutory matrices. And finally, you will find the formula of an involutory matrix and all the properties of this type of matrices.

Table of Contents

What is an involutory matrix?

The definition of involutory matrix is as follows:

An involutory matrix is a square and invertible matrix whose inverse matrix is the matrix itself.

Obviously, to fully understand what an involutory matrix is, you must know what the inverse of a matrix is. Here you can see how to find the inverse of a 3×3 matrix.

So, all involutory matrices matrix meet the following condition:

$A^{-1}=A$

Therefore, any involutory matrix is a nondegenerate matrix.

It can be easily deduced that when a matrix is involutory, multiplying the matrix by the matrix itself results in the identity matrix. Below you can see the proof:

Any matrix multiplied by its inverse gives the Identity (or Unit) matrix:

$\displaystyle A\cdot A^{-1}=I$

Since the inverse of an involutory matrix is the matrix itself:

$\displaystyle A \cdot A = I$

Therefore, an involutory matrix squared gives the identity matrix:

$\displaystyle A^2=I$

See: what is the identity matrix?

Examples of involutory matrices

Once we have seen the meaning of involutory matrix, let’s see some examples of involutory matrices to fully understand the concept:

Example of a 2×2 involutory matrix

example of a 2x2 dimension involutory matrix

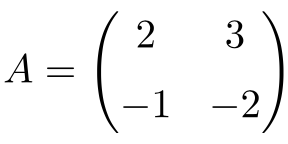
We can prove that it is an involutory matrix by calculating the square of the matrix:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Since matrix A squared is the identity matrix, matrix A is a 2×2 involutory matrix.

Example of a 3×3 involutory matrix

example of a 3x3 dimension involutory matrix

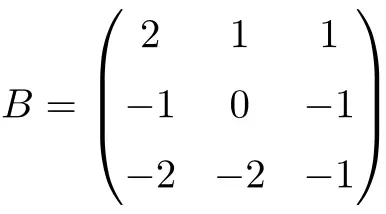
We can verify that it is an involutory matrix by computing the product of the matrix by itself:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Since matrix B raised to 2 results in the identity matrix, matrix B is a 3×3 involutory matrix.

Example of a 4×4 involutory matrix

The Identity (or Unit) matrix, whatever its dimension, is an involutory matrix by definition.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

We can check that it is an involutory matrix by raising the matrix to 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Since the result of the power is the identity matrix itself, this type of matrix is an involutory matrix.

Formula for a 2×2 involutory matrix

The formula for a 2×2 involutory matrix is as follows:

In other words, any 2×2 matrix whose entries on the main diagonal are opposite and its determinant is -1 is an involutory matrix.

However, in addition to the matrices described by this formula, you must bear in mind that the identity matrix and its opposite are also involutory matrices of order 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Properties of an involutory matrix

Involutory matrices have the following characteristics:

The determinant of an involutory matrix is always equal to -1 or +1.

There is a relationship between involutory matrices and idempotent matrices: matrix $A$ is involutory if, and only if, matrix $\displaystyle Q =\frac{1}{2}\cdot(A+I)$ is idempotent.

See: example of idempotent matrix

If $A$ and $B$ are two involutory matrices that commute with each other, then the matrix product $AB$ results in an involutory matrix.

Any power of an involutory matrix gives another involutory matrix. In particular, an involutory matrix raised to an odd exponent will be equal to itself, and on the other hand, if it is raised to an even exponent it will be equal to the Identity matrix.

$A^2 = I$

$A^3 = A$