▷ What is a Unitary matrix? (With examples and its properties)

On this post we explain what the unitary matrix is and, in addition, we analyze several examples to fully understand its meaning. You will also find all the properties of this type of matrix.

Table of Contents

What is a unitary matrix?

The definition of unitary matrix is as follows:

A unitary matrix is a complex matrix that multiplied by its conjugate transpose is equal to the identity matrix, thus, the conjugate transpose of a unitary matrix is also its inverse. That is, the following condition is met:

$U \cdot U^H = U^H \cdot U = I$

Where U is a unitary matrix and U^H its conjugate transpose.

See: complex conjugate transpose of a matrix.

The condition of unitary matrix implies that the inverse of a unitary matrix is also its conjugate transpose because, by the definition of an inverse matrix, a matrix is an inverse of another if its product results in the Identity matrix.

$\left. \begin{array}{c} U \cdot U^H = I \\[2ex] U \cdot U ^{-1} = I \end{array} \right\} \longrightarrow \ U^H = U^{-1}$

So a unitary matrix will always be a non-degenerate matrix.

On the other hand, the analog of the unitary matrix in a real number field is the orthogonal matrix.

Examples of unitary matrices

Example of a 2×2 unitary matrix

Once we have seen the concept of a unitary matrix, we are going to see an example of a 2×2 unitary matrix to understand it better:

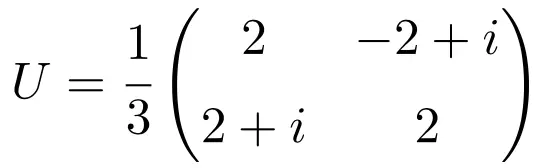
This matrix is unitary because the multiplication of itself by its conjugate matrix results in the identity (or unit) matrix:

$\displaystyle U\cdot U^H=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

And, as we have seen before, any unitary commutes with its conjugate transpose:

$\displaystyle U^H\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Example of a diagonal unitary matrix

The diagonal matrix composed only of the complex number i is also an example of a unitary matrix, regardless of the dimension of the matrix. Below you have a solved exercise exemplifying this theorem with a unitary matrix of dimension 3×3:

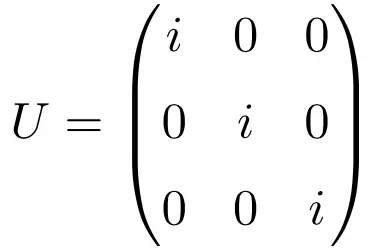
Note that if we calculate the product of the matrix by its conjugate transpose, it gives the identity matrix as a solution:

$\displaystyle U\cdot U^H =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

And the same happens if we multiply the matrices in the inverted order:

$\displaystyle U^H\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

Therefore, as long as the matrix is formed by the imaginary number i in the main diagonal and the rest of the elements are zero (0), it will be a unitary matrix.

Properties of a unitary matrix

The characteristics of unitary matrices are as follows:

Obviously, every unitary matrix is a normal matrix. Although not all normal matrices are unitary matrices.

Unitary matrices are always square matrices.

All unitary matrices are diagonalizable.

The absolute value of the determinant of a unitary matrix is always equal to 1.

$\begin{vmatrix} det(U) \end{vmatrix} = 1$

The identity matrix is a unitary matrix.

For any integer $n$ , the set of all $n \times n$ unitary matrices together with the matrix product operation form a group, called the unitary group.

So the multiplication of two unitary matrices of the same order results in another unitary matrix.

The modulus of all eigenvalues of a unitary matrix is always equal to 1.

$\begin{vmatrix} \lambda \end{vmatrix} = 1$

The eigenspaces of this type of matrix are orthogonal.

What is a unitary matrix?

Examples of unitary matrices

Example of a 2×2 unitary matrix

Example of a diagonal unitary matrix

Properties of a unitary matrix

Leave a Comment Cancel Reply