On this post you will see what a skew-Hermitian matrix is, also called antihermitian matrix. You will find examples of skew-Hermitian matrices, all their properties and the formula of this type of square complex matrices. Finally, you will find the explanation of how to decompose any complex matrix into the sum of a skew-Hermitian matrix plus another Hermitian matrix.
Table of Contents
What is a skew-Hermitian (or antihermitian) matrix?
The definition of skew-Hermitian matrix is as follows:
A skew-Hermitian matrix, also called an antihermitian matrix, is a square matrix with complex numbers whose conjugate transpose is equal to the same matrix but changed sign. That is, all skew-Hermitian matrices meet the following condition:
Where AH is the conjugate transpose of matrix A.
See: how to calculate the conjugate transpose of a matrix.
As a curiosity, this type of matrix is said in this way because it fulfills the opposite condition to the Hermitian matrix, whose name comes from the important French mathematician Charles Hermite, a professor and researcher of mathematics of the 19th century who did important studies particularly in the field of linear algebra.
Examples of skew-Hermitian matrices
Once we have seen the definition of a skew-Hermitian matrix (or antihermitian matrix) we are going to see some examples of skew-Hermitian matrices of different dimensions:
Example of a 2×2 skew-Hermitian matrix
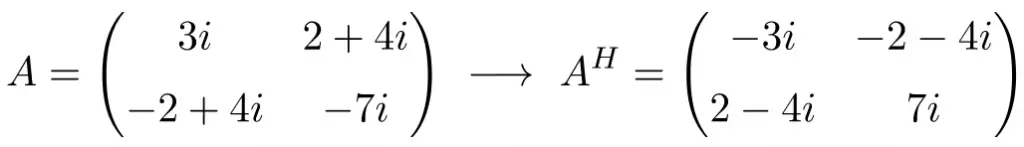
Example of a 3×3 skew-Hermitian matrix
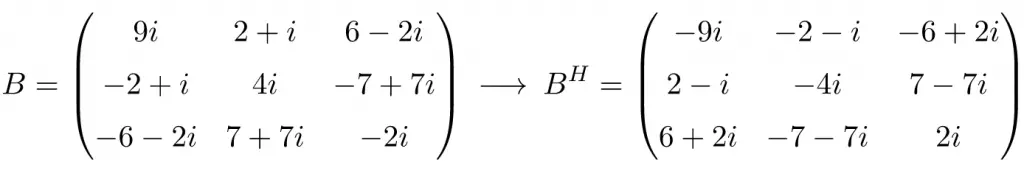
Example of a 4×4 skew-Hermitian matrix
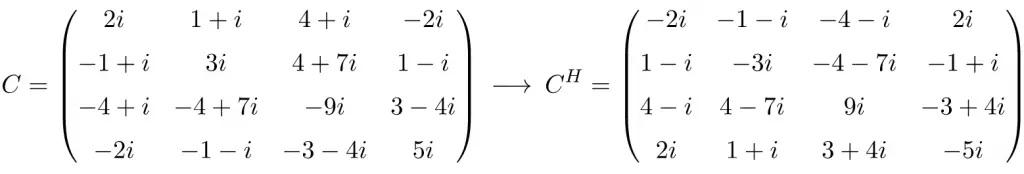
As you can see, matrices A, B and C are skew-Hermitian because the conjugate transpose of each matrix is equal to the negative of each original matrix.
Properties of the skew-Hermitian matrix
The characteristics of the skew-Hermitian matrix are as follows:
- Every skew-Hermitian matrix is an example of a normal matrix. Although not all normal matrices are skew-Hermitian matrices.
- Any skew-Hermitian matrix is diagonalizable. Furthermore, the obtained diagonal matrix only contains purely imaginary elements.
- Therefore, the eigenvalues of a skew-Hermitian matrix are always imaginary numbers.
- The eigenvectors of different eigenvalues of a skew-Hermitian matrix are orthogonal.
- A matrix of real numbers, that is, that no element has imaginary part, is skew-Hermitian if, and only if, it is an antisymmetric matrix.
- A skew-Hermitian matrix can be expressed as the sum of a real antisymmetric matrix plus an imaginary symmetric matrix.
- The sum (or subtraction) of two skew-Hermitian matrices is equal to another skew-Hermitian matrix.
- The result of the product of a skew-Hermitian matrix and a scalar is another skew-Hermitian matrix if the scalar is a real number.
- The power of a skew-Hermitian matrix is equal to a skew-Hermitian matrix if the exponent is odd, on the other hand, if it is raised to an even exponent, the result will be a Hermitian matrix.
- If
is a skew-Hermitian matrix, then the product 
is a Hermitian matrix.
Formula of a skew-Hermitian matrix
If you have paid attention at the examples above, skew-Hermitian matrices always have the same structure: they are formed by imaginary numbers (without real part) on the main diagonal, and the complex element located in the i-th row and the j-th column must have the same imaginary part and the same real part but changed sign as the element of the j-th row and the i-th column.
Although written may seem a bit complicated, you will understand it better with the formula of skew-Hermitian matrices:
![\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}](https://www.algebrapracticeproblems.com/wp-content/ql-cache/quicklatex.com-5fe64cb90d3d22fca7da910b85d82f31_l3.svg "Rendered by QuickLaTeX.com")
As you can see, the elements of the main diagonal of a skew-Hermitian matrix are totally imaginary and the elements of the secondary diagonal have the same imaginary part and the real part changed sign.
Therefore, the real part of an skew-Hermitian matrix must be antisymmetric and the imaginary part symmetric.
Decomposition of a complex matrix into a skew-Hermitian and a Hermitian matrix
Any matrix that contains complex numbers can be decomposed into the sum of a skew-Hermitian matrix plus another Hermitian matrix. But to perform this we must know the following characteristics of these types of matrices:
- The sum of a square complex matrix plus its conjugate transpose results in a Hermitian matrix:
- The difference between a square complex matrix and its conjugate transpose is equal to a skew-Hermitian matrix:
- Thus, all complex matrices can be decomposed into the sum of a Hermitian and a skew-Hermitian matrix. This theorem is known as the Teoplitz decomposition:
![\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^H) \qquad B = \cfrac{1}{2} \cdot (C-C^H)\end{array}](https://www.algebrapracticeproblems.com/wp-content/ql-cache/quicklatex.com-edde96e50751f80560db75499e16cb86_l3.svg "Rendered by QuickLaTeX.com")
Where C is the complex matrix that we want to decompose, CH its conjugate transpose, and finally A and B are the Hermitian and the skew-Hermitian matrices respectively into which matrix C is decomposed.
