▷ Normal matrix: definition, examples, properties, exercises,...

On this post you will find what a normal matrix is, as well as examples of normal matrices. In addition, you will find the properties of this type of matrix and exercises solved step by step.

Table of Contents

What is a normal matrix?

The definition of normal matrix is as follows:

A normal matrix is a complex matrix that multiplied by its conjugate transpose matrix is equal to the product of the conjugate transpose by itself. That is, all normal matrices meet the following condition:

$A \cdot A^H = A^H \cdot A$

Where A^H is the conjugate transpose matrix of A.

However, in the real numbers field the previous condition is the same as saying that a matrix commutes with its transpose, that is:

$A\cdot A^T=A^T\cdot A$

Since the conjugate transpose matrix of a real matrix is simply the transpose of the matrix.

Examples of normal matrices

Once we have seen the meaning of normal matrix, let’s see some examples of this type of matrix to fully understand the concept:

Example of a normal matrix with complex numbers

The following complex square matrix of dimension 2×2 is normal:

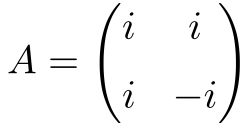
Below there is the demonstration of the normality of the matrix:

$\displaystyle A\cdot A^H = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^H\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

Example of a normal matrix with real numbers

The following square matrix with real numbers of order 2 is also normal:

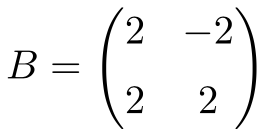
In this case, as it only has real numbers, to show that it is normal we just have to check that the matrix commutes with its transpose:

$\displaystyle B\cdot B^T = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^T\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

Properties of normal matrices

Normal matrices have the following characteristics:

Every normal matrix is diagonalizable.

Every Unitary matrix is also a normal matrix.

Similarly, a self-adjoint matrix is a normal matrix.

A skew-Hermitian matrix is a normal matrix.

If A is a normal matrix, the eigenvalues of the conjugate transpose matrix A^H are the conjugate eigenvalues of A.

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^H=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^H,1} = 0 \ ; \ \lambda_{A^H,2} = -3i$

The eigenvectors of any normal matrix associated with different eigenvalues are orthogonal.

If a matrix is a symmetric real matrix, it is a normal matrix at the same time.

Similarly, an antisymmetric real matrix is also a normal matrix.

Lastly, any orthogonal matrix formed by real numbers is also a normal matrix.

See definition of orthogonal matrix.

Solved exercises of normal matrices

Exercise 1

Check that the following complex matrix of order 2 is normal:

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

See solution

To prove that the matrix is normal we must first calculate its conjugate transpose:

$\displaystyle A^H=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

And now we do the check by multiplying matrix A by matrix A^H in the two possible orders:

$\displaystyle A\cdot A^H = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^H\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

The result of both multiplications is equal, thus, matrix A is normal.

Exercise 2

Show that the following square real matrix of order 2 is normal:

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

See solution

In this problem the matrix has only real numbers, so it is enough to check that the matrix product between matrix A and its tranpose is the same regardless of the order of the multiplication:

$\displaystyle A\cdot A^T = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^T\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

The result of both products is the same, therefore, matrix A is normal.

Exercise 3

Determine whether the following matrix of complex numbers is normal:

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

See solution

To verify that the matrix is normal we must first calculate its conjugate transpose:

$\displaystyle A^H=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

And now we check whether matrix A and its conjugate transpose commutate:

$\displaystyle A\cdot A^H = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^H\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

The result of both multiplications is the same, so matrix A is normal.

Exercise 4

Verify that the following 3×3 dimension real matrix is normal:

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

See solution

As the matrix is completely made up of real elements, it is sufficient to check that the matrix product between matrix A and its transpose is independent of the multiplication order:

$\displaystyle A\cdot A^T = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^T\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

The result of both products is identical, so matrix A is normal.

Exercise 5

Determine if the following complex matrix of order 3 is normal:

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

See solution

First, we calculate the conjugate transpose of the matrix:

$\displaystyle A^H=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Now we should do the matrix multiplications between matrix A and its conjugate transpose in the two possible orders. However, the conjugate transpose matrix of A is equal to the matrix A itself, therefore this is a Hermitian matrix. And consequently, from the properties of normal matrices it follows that A is a normal matrix, because any Hermitian matrix is a normal matrix.

What is a normal matrix?

Examples of normal matrices

Example of a normal matrix with complex numbers

Example of a normal matrix with real numbers

Properties of normal matrices

Solved exercises of normal matrices

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Leave a Comment Cancel Reply