Here you will find what a complex matrix is and all its characteristics. Also, you will see the different types of complex matrices and examples. Finally, we’ll explain how to calculate operations with complex matrices.
Table of Contents
What is a complex matrix?
The definition of complex matrix is as follows.
A complex matrix is a matrix that has some complex number among its elements.
Remember that a complex or imaginary number is a number made up of a real part and an imaginary part, which is indicated by the letter i. For example:
The real part of the complex number above is 3, and its imaginary part is 5.
Examples of complex matrices
Once we have seen the meaning of complex matrix, let’s look at some examples of complex matrices of different dimensions:
Example of a 2×2 complex matrix
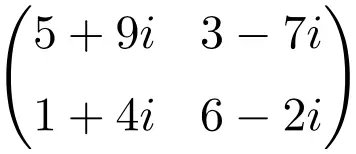
Example of a 3×3 complex matrix
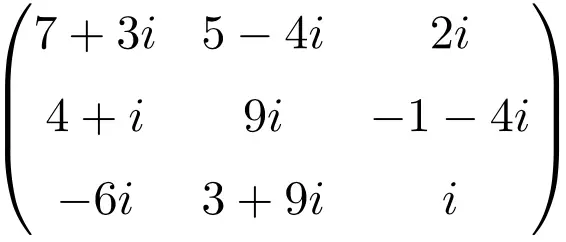
Example of a 4×4 complex matrix
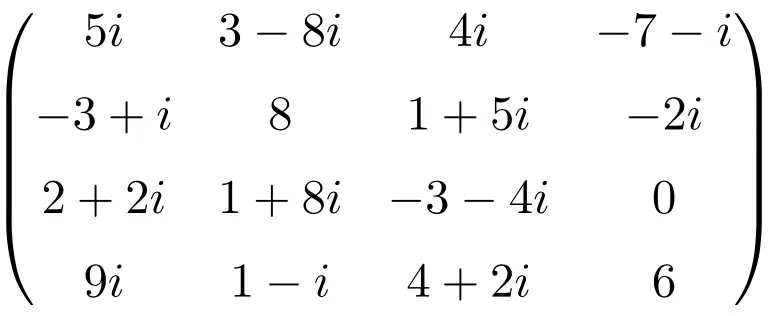
Types of complex matrices
The different types of complex matrices are the following:
- Conjugate matrix: complex matrix which all its elements have been replaced by their complex conjugates, that is, the sign of the imaginary part of all its complex numbers have been changed. Click the following link to see a conjugate matrix example.
- Conjugate transpose matrix: complex matrix which has been transposed and then each entry has been replaced by its complex conjugate. In the following link you can see how to find the conjugate transpose of a complex matrix.
- Normal matrix: complex matrix that multiplied by its conjugate transpose equals to the product of the conjugate transpose by itself. A normal matrix can also be composed of only real numbers. For more about it, see examples of Normal matrices.
- Unitary matrix: complex matrix that multiplied by its conjugate transpose is equal to the identity matrix. The properties of this type of complex matrix are quite interesting, for example the conjugate transpose of a unitary matrix is also its inverse. See all the Unitary matrix properties.
- Hermitian matrix: square complex matrix that is equal to its conjugate transpose. Hermitian matrices are also called self-adjoint matrices. See a Hermitian matrix example.
- Skew-Hermitian matrix: square complex matrix whose conjugate transpose results in the same matrix but changed sign. It is also called antihermitian matrix. Click the following link to see examples and all the properties of a skew-Hermitian matrix.
Operations with complex matrices
Operations with complex matrices are calculated in the same way as non-complex matrices (or real matrices). However, you have to know how to calculate operations with complex numbers. Let’s see one example for each type of complex matrix operation:
- Complex matrices addition:
- Complex matrices subtraction:
- Complex matrices multiplication:
- Determinant of a complex matrix:
- Inverse of a complex matrix:
👉👉👉 If you have any doubt about how to perform all these operations with matrices, you can look for each operation in our search engine. 🔎
